- ГОЛОНОМНАЯ СИСТЕМА
система материальных точек, либо не стесненная никакими связями, либо стесненная только геометрнч. связями, накладывающими ограничения на положения точек системы и могущими быть представленными в форме конечных соотношений вида
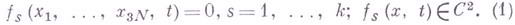
Здесь t обозначает время, х i - декартовы координаты точек, N - число точек системы. Если
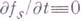 , то связи наз. стационарными, в противном случае - нестационарными. Всякое положение системы, для к-рого координаты точек удовлетворяют уравнениям (1), наз. возможным для данного момента t. Связи (1) налагают ограничения не только на положения
, то связи наз. стационарными, в противном случае - нестационарными. Всякое положение системы, для к-рого координаты точек удовлетворяют уравнениям (1), наз. возможным для данного момента t. Связи (1) налагают ограничения не только на положения 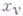 , но и на скорости vv и ускорения
, но и на скорости vv и ускорения 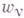 точек вида
точек вида
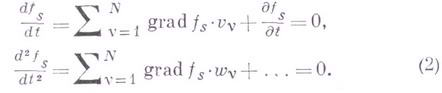
Скорости и ускорения, удовлетворяющие уравнениям (2), наз. кинематически возможными в данном положении
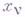 системы для данного момента t. Бесконечно малые перемещения
системы для данного момента t. Бесконечно малые перемещения 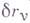 , удовлетворяющие условиям вида .
, удовлетворяющие условиям вида .
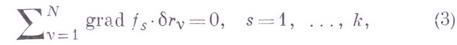
представляют собою возможные (виртуальные) перемещения системы, в отличие от действительных перемещений
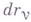 , совершаемых системой за время
, совершаемых системой за время 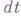 под действием приложенных к ней сил и удовлетворяющих условиям вида
под действием приложенных к ней сил и удовлетворяющих условиям вида
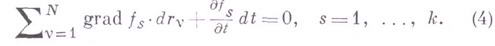
Для стационарных связей действительные перемещения находятся среди возможных, для нестационарных - вообще говоря, не находятся. Возможные перемещения способны перевести голономную систему из одного возможного для данного tположения системы в любое другое бесконечно близкое положение, возможное для того же момента t.
Число независимых вариаций координат точек системы наз. числом ее степеней свободы, для голономной системы оно совпадает с числом
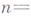
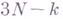 независимых произвольных параметров
независимых произвольных параметров 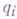 , с помощью к-рых уравнения (1) связей можно представить в форме конечных соотношений вида
, с помощью к-рых уравнения (1) связей можно представить в форме конечных соотношений вида
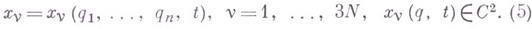
Параметры
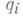 носят название обобщенных, или лагранжевых координат системы; их называют также голономными координатами^ отличие отнеголономных координат, или квазикоординат
носят название обобщенных, или лагранжевых координат системы; их называют также голономными координатами^ отличие отнеголономных координат, или квазикоординат 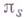 , вводимых неинтегрируемыми соотношениями вида
, вводимых неинтегрируемыми соотношениями вида
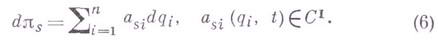
Связи, аналитически выражаемые уравнениями (1), носят название удерживающих, или двусторонних связей, в отличие от неудерживающих, или односторонних связей, выражаемых неравенствами вида
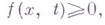
и накладывающих следующие условия на возможные перемещения
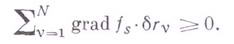
Возможные перемещения системы с двусторонними связями обратимы, среди возможных перемещений систем с односторонними связями имеются необратимые (см. [1]).
Движения голономных систем описываются Лагранжа уравнениями(1-го и 2-го рода), Гамильтона уравнениями в лагранжевых координатах и импульсах, Аппеля уравнениями, Пуанкаре уравнениями или Четаева уравнениями в лагранжевых координатах и квазикоординатах.
Лит.:[1] Суслов Г. К., Теоретическая механика, 3 изд., М., 1944. В. В. Румянцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
