МАШИНЫ И МЕХАНИЗМЫ

механические устройства, облегчающие труд и повышающие его производительность. Машины могут быть разной степени сложности - от простой одноколесной тачки до лифтов, автомобилей, печатных, текстильных, вычислительных машин. Энергетические машины преобразуют один вид энергии в другой. Например, генераторы гидроэлектростанции преобразуют механическую энергию падающей воды в электрическую энергию. Двигатель внутреннего сгорания преобразует химическую энергию бензина в тепловую, а затем в механическую энергию движения автомобиля
(см. также
ЭЛЕКТРОМАШИННЫЕ ГЕНЕРАТОРЫ И ЭЛЕКТРОДВИГАТЕЛИ;
ДВИГАТЕЛЬ ТЕПЛОВОЙ;
ТУРБИНА).
Так называемые рабочие машины преобразуют свойства или состояние материалов (металлорежущие станки, транспортные машины) либо информацию (вычислительные машины). Машины состоят из механизмов (двигательного, передаточного и исполнительного) - многозвенных устройств, передающих и преобразующих силу и движение. Простой механизм, называемый полиспастом
(см. БЛОКИ И ПОЛИСПАСТЫ),
увеличивает силу, приложенную к грузу, и за счет этого позволяет вручную поднимать тяжелые предметы. Другие механизмы облегчают работу, увеличивая скорость. Так, велосипедная цепь, входящая в зацепление со звездочкой, преобразует медленное вращение педалей в быстрое вращение заднего колеса. Однако механизмы, увеличивающие скорость, делают это за счет уменьшения силы, а увеличивающие силу - за счет уменьшения скорости. Увеличить одновременно и скорость и силу невозможно. Механизмы могут также просто изменять направление силы. Пример - блок на конце флагштока: чтобы поднять флаг, тянут за шнур вниз. Изменение направления может сочетаться с увеличением силы или скорости. Так, тяжелый груз можно приподнять, нажимая на рычаг вниз.
ОСНОВНЫЕ ПРИНЦИПЫ РАБОТЫ МАШИН И МЕХАНИЗМОВ
Основной закон. Хотя механизмы и позволяют получить выигрыш в силе или скорости, возможности такого выигрыша ограничиваются законом сохранения энергии. В применении к машинам и механизмам он гласит: энергия не может ни возникать, ни исчезать, она может быть лишь преобразована в другие виды энергии или в работу. Поэтому на выходе машины или механизма не может оказаться больше энергии, чем на входе. К тому же в реальных машинах часть энергии теряется из-за трения. Поскольку работа может быть превращена в энергию и наоборот, закон сохранения энергии для машин и механизмов можно записать в виде Работа на входе = Работа на выходе + Потери на трение. Отсюда видно, в частности, почему невозможна машина типа вечного двигателя: из-за неизбежных потерь энергии на трение она рано или поздно остановится.
Выигрыш в силе или скорости. Механизмы, как указывалось выше, могут применяться для увеличения силы или скорости. Идеальный, или теоретический, выигрыш в силе или скорости - это коэффициент увеличения силы или скорости, который был бы возможен в отсутствие потерь энергии, обусловленных трением. Идеальный выигрыш на практике недостижим. Реальный выигрыш, например в силе, равен отношению силы (называемой нагрузкой), которую развивает механизм, к силе (называемой усилием), которая прикладывается к механизму.
Механический КПД. Коэффициентом полезного
действия машины называется процентное отношение работы на ее выходе к работе на ее входе. Для механизма КПД равен отношению реального выигрыша к идеальному. КПД рычага может быть очень высоким - до 90% и даже больше. В то же время КПД полиспаста из-за значительного трения и массы движущихся частей обычно не превышает 50%. КПД домкрата может составлять лишь 25% из-за большой площади контакта между винтом и его корпусом, а следовательно, большого трения. Это приблизительно такой же КПД, как у автомобильного двигателя. См. АВТОМОБИЛЬ ЛЕГКОВОЙ. КПД можно в известных пределах повысить, уменьшив трение за счет смазки и применения подшипников качения. См. также СМАЗКА.
ПРОСТЕЙШИЕ МЕХАНИЗМЫ
Простейшие механизмы можно найти почти в любых более сложных машинах и механизмах. Их всего шесть: рычаг, блок, дифференциальный ворот, наклонная плоскость, клин и винт. Некоторые авторитетные специалисты утверждают, что на самом деле можно говорить всего лишь о двух простейших механизмах - рычаге и наклонной плоскости, - так как нетрудно показать, что блок и ворот представляют собой варианты рычага, а клин и винт - варианты наклонной плоскости.
Рычаг. Это жесткий стержень, который может свободно поворачиваться относительно неподвижной точки, называемой точкой опоры. Примером рычага могут служить лом, молоток с расщепом, тачка, метла. Рычаги бывают трех родов, различающихся взаимным расположением точек приложения нагрузки и усилия и точки опоры (рис. 1). Идеальный выигрыш в силе рычага равен отношению расстояния DE от точки приложения усилия до точки опоры к расстоянию DL от точки приложения нагрузки до точки опоры. Для рычага I рода расстояние DE обычно больше DL, а поэтому идеальный выигрыш в силе больше 1. Для рычага II рода идеальный выигрыш в силе тоже больше единицы. Что же касается рычага III рода, то величина DE для него меньше DL, а стало быть, больше единицы выигрыш в скорости.

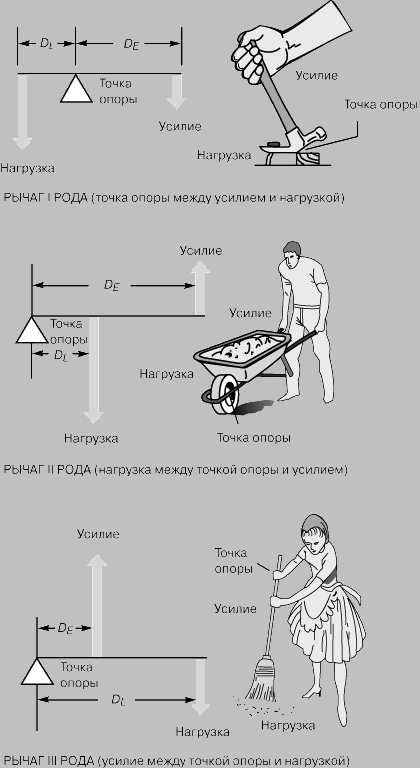
Рис. 1. РЫЧАГИ I, II И III РОДА

Блок. Это колесо с желобом по окружности для каната или цепи. Блоки применяются в грузоподъемных устройствах. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспастом. Одиночный блок может быть либо с закрепленной осью (уравнительным), либо подвижным (рис. 2). Блок с закрепленной осью действует как рычаг I рода с точкой опоры на его оси. Поскольку плечо усилия равно плечу нагрузки (радиус блока), идеальный выигрыш в силе и скорости равен 1. Подвижный же блок действует как рычаг II рода, поскольку нагрузка расположена между точкой опоры и усилием. Плечо нагрузки (радиус блока) вдвое меньше плеча усилия (диаметр блока). Поэтому для подвижного блока идеальный выигрыш в силе равен 2.

Рис. 2. БЛОК может быть закрепленным (уравнительным) или подвижным. Уравнительный блок действует как рычаг I рода, а подвижный - как рычаг II рода.

Более простой способ определения идеального выигрыша в силе для блока или системы блоков - по числу параллельных концов каната, удерживающих нагрузку, как это нетрудно сообразить, взглянув на рис. 2. Уравнительные и подвижные блоки можно сочетать по-разному для увеличения выигрыша в силе. В одной обойме можно установить два, три или большее число блоков, а конец троса можно прикрепить либо к неподвижной, либо к подвижной обойме.
Дифференциальный ворот. Это, в сущности, два колеса, соединенные вместе и вращающиеся вокруг одной оси (рис. 3), например, колодезный ворот с ручкой.

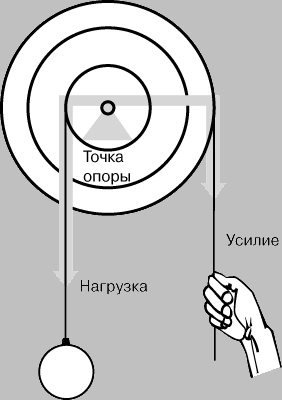
Рис 3. ВОРОТ, действующий как рычаг I рода, представляет собой, в сущности, два скрепленных вместе колеса, вращающихся вокруг общей оси.

Дифференциальный ворот может давать выигрыш как в силе, так и в скорости. Это зависит от того, где прилагается усилие, а где - нагрузка, поскольку он действует как рычаг I рода. Точка опоры расположена на закрепленной (фиксированной) оси, а поэтому плечи усилия и нагрузки равны радиусам соответствующих колес. Пример такого устройства для выигрыша в силе - отвертка, а для выигрыша в скорости - шлифовальный круг.
Зубчатые колеса. Система двух находящихся в зацеплении зубчатых колес, сидящих на валах одинакового диаметра (рис. 4), в какой-то мере аналогична дифференциальному вороту (см. также ЗУБЧАТАЯ ПЕРЕДАЧА). Скорость вращения колес обратно пропорциональна их диаметру. Если малая ведущая шестерня A (к которой приложено усилие) по диаметру вдвое меньше большого зубчатого колеса B, то она должна вращаться вдвое быстрее. Таким образом, выигрыш в силе такой зубчатой передачи равен 2. Но если точки приложения усилия и нагрузки поменять местами, так что колесо B станет ведущим, то выигрыш в силе будет равен 1/2, а выигрыш в скорости - 2.

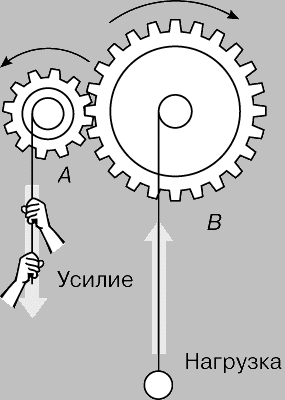
Рис. 4. ЗУБЧАТЫЕ КОЛЕСА, действующие в принципе так же, как и ворот, могут давать как выигрыш в силе, так и выигрыш в скорости.

Наклонная плоскость. Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия. К таким устройствам относятся пандусы, эскалаторы, обычные лестницы, а также конвейеры (с роликами для уменьшения трения). Идеальный выигрыш в силе, обеспечиваемый наклонной плоскостью (рис. 5), равен отношению расстояния, на которое перемещается нагрузка, к расстоянию, проходимому точкой приложения усилия. Первое есть длина наклонной плоскости, а второе - высота, на которую поднимается груз. Поскольку гипотенуза больше катета, наклонная плоскость всегда дает выигрыш в силе. Выигрыш тем больше, чем меньше наклон плоскости. Этим объясняется то, что горные автомобильные и железные дороги имеют вид серпантина: чем меньше крутизна дороги, тем легче по ней подниматься.

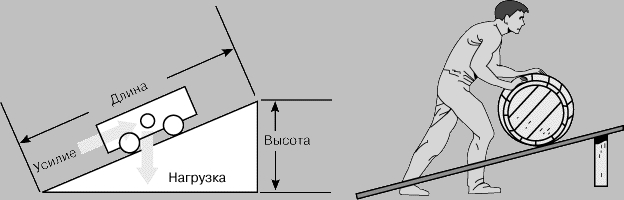
Рис. 5. НАКЛОННАЯ ПЛОСКОСТЬ дает выигрыш в силе, равный (в идеале) отношению длины к высоте.

Клин. Это, в сущности, сдвоенная наклонная плоскость (рис. 6). Главное его отличие от наклонной плоскости в том, что она обычно неподвижна, и груз под действием усилия движется по ней, а клин вгоняют под нагрузку или в нагрузку. Принцип клина используется в таких инструментах и орудиях, как топор, зубило, нож, гвоздь, швейная игла.

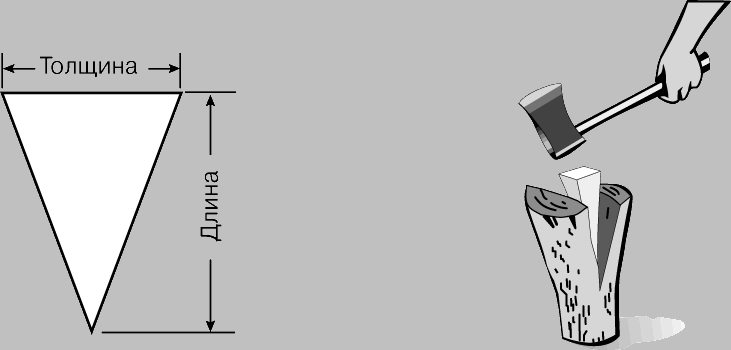
Рис. 6. КЛИН - как бы сдвоенная наклонная плоскость. Идеальный выигрыш в силе равен отношению длины клина к толщине на тупом конце.

Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце. Реальный выигрыш клина, в отличие от других простейших механизмов, трудно определить. Сопротивление, встречаемое им, непредсказуемо меняется для разных участков его "щек". Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения.
Винт. Резьба винта (рис. 7) - это, в сущности, наклонная плоскость, многократно обернутая вокруг цилиндра. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой (A) или правой (B). Сопрягающаяся деталь, естественно, должна иметь резьбу такого же направления. Примеры простых устройств с винтовой резьбой - домкрат, болт с гайкой, микрометр, тиски.

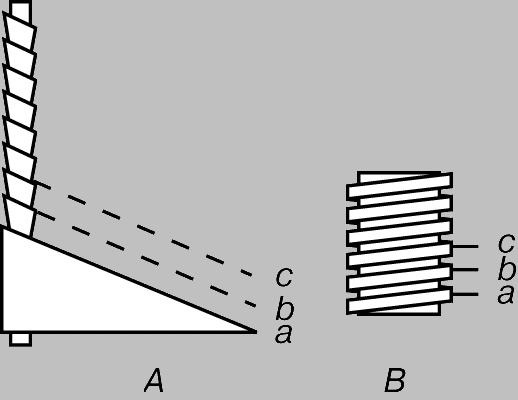
Рис. 7. ВИНТ с прямоугольной резьбой - по существу, наклонная плоскость, многократно обернутая вокруг цилиндра. A - левая, B - правая резьба.

Поскольку резьба - наклонная плоскость, она всегда дает выигрыш в силе. Идеальный выигрыш равен отношению расстояния, проходимого точкой приложения усилия за один оборот винта (длины окружности), к расстоянию, проходимому при этом нагрузкой по оси винта. За один оборот нагрузка перемещается на расстояние между двумя соседними витками резьбы (a и b или b и c на рис. 7), которое называется шагом резьбы. Шаг резьбы обычно значительно меньше ее диаметра, так как иначе слишком велико трение.
КОМБИНИРОВАННЫЕ МЕХАНИЗМЫ
Комбинированный механизм состоит из двух или большего числа простых. Это не обязательно сложное устройство; многие довольно простые механизмы тоже можно считать комбинированными. Например, в мясорубке имеются ворот (ручка), винт (проталкивающий мясо) и клин (нож-резак). Стрелки наручных часов поворачиваются системой зубчатых колес разного диаметра, находящихся в зацеплении друг с другом. Один из наиболее известных несложных комбинированных механизмов - домкрат. Домкрат (рис. 8) представляет собой комбинацию винта и ворота. Головка винта подпирает нагрузку, а другой его конец входит в резьбовую опору. Усилие прилагается к рукоятке, закрепленной в головке винта. Таким образом, расстояние усилия равно длине окружности, описываемой концом ручки. Длина окружности дается выражением 2pr, где p = 3,14159, а r - радиус окружности, т.е. в данном случае длина ручки. Очевидно, что чем длиннее ручка, тем больше идеальный выигрыш в силе. Расстояние, проходимое нагрузкой за один оборот ручки, равно шагу резьбы. В идеале можно получить очень большой выигрыш в силе, если длинную ручку сочетать с малым шагом резьбы. Поэтому несмотря на малый КПД домкрата (около 25%) он дает большой реальный выигрыш в силе.

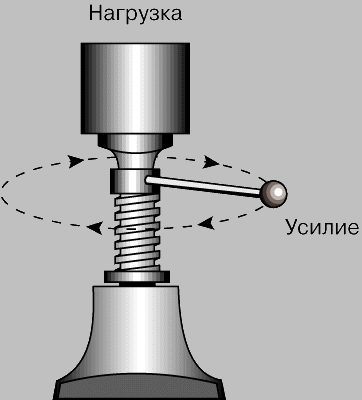
Рис. 8. ДОМКРАТ - пример несложного комбинированного механизма (сочетание винта и ворота).

Выигрыш в силе, создаваемый комбинированным механизмом, равен произведению выигрышей отдельных механизмов, входящих в его состав. Так, идеальный выигрыш в силе (ИВС) для домкрата равен отношению длины окружности, описываемой ручкой, к шагу резьбы. Для входящего в состав домкрата ворота ИВС равен отношению длины окружности, описываемой ручкой (расстояние усилия), к длине окружности винта (расстояние нагрузки). Для винта домкрата ИВС равен отношению длины окружности винта (расстояния усилия) к шагу резьбы винта (расстоянию нагрузки). Перемножая ИВС отдельных механизмов домкрата, получаем для комбинированного механизма ИВС = (Окружность ручки/Окружность винта) * (Окружность винта/Шаг резьбы) = (Окружность ручки/Шаг резьбы). Для более сложных комбинированных механизмов вычислить ИВС труднее. Поэтому для них обычно указывают лишь реальный выигрыш.
См. также
КУЛАЧКОВЫЙ МЕХАНИЗМ;
ДИНАМИКА;
СТАНКИ МЕТАЛЛОРЕЖУЩИЕ;
МЕХАНИКА.
ЛИТЕРАТУРА
Попов С.А. Курсовое проектирование по теории механизмов и машин. М., 1986