РАУЛЯ ЗАКОН

РАУЛЯ ЗАКОН

: относит. понижение парциального давления пара р-ритсля над разб. бинарным р-ром неэлектролита равно молярной доле растворенного в-ва x в:

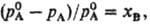
4040-3.jpg

где р А-> парциальное давление р-рителя, 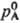4040-4.jpg -давление на-сыщ. пара чистого р-рителя. Соотв. для молярной доли р-рителя xA можно записать:

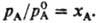
4040-5.jpg

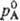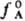Если пар над р-ром нельзя считать идеальным газом, давления 4040-6.jpg и р А заменяют на фугитивности f А и 4040-8.jpg:

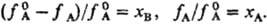
4040-7.jpg

Р-ры, для к-рых Р. з. выполняется во всем интервале концентраций для обоих компонентов, наз. идеальными (совершенными). Для идеального р-ра термодинамич. активность компонента a А равна его молярной доле х А (а А = = x А), а хим. потенциал компонента, по определению, равен:

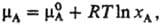
4040-9.jpg

где Т-абс. т-ра, R-газовая постоянная,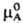4040-10.jpg -стандартный хим. потенциал (см. Стандартное состояние).Парциальное давление растворенного в-ва при постоянной т-ре пропорционально его молярной доле (см. Генри закон), зависимость осмотич. давления р-ра от концентрации растворенного в-ва выражается законом Вант-Гоффа (см. Оcмос).

Положительные (а)и отрицательные (б)отклонения р-ра от идеальности. На оси абсцисс отложена молярная доля р-рителя (компонент А), по оси ординат-парциальное давление растворенного в-ва (компонент В). Пунктиром показаны соответствующие зависимости для идеального р-ра.

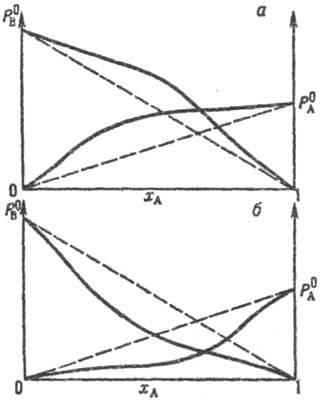
4040-11.jpg

Для мн. бинарных систем-жидких и твердых р-ров, расплавов, многокомпонентных смесей - Р. з. выполняется с достаточной точностью и служит хорошим приближением для определения парциальных давлений при молярной доле растворенного в-ва до 0,1-0,5. Если парциальные давления компонентов выше значений, предсказываемых Р. з., говорят о положит. отклонениях от идеальности, если ниже-об отрицат. отклонениях. Для смесей орг. в-в типа С 6 Н 6 -(СН 3)2 СО, (С 2 Н 5)2 О-СНС13 отклонение от идеальности не превышает 100% (см. рис.). При сильном взаимод. компонентов, напр. в случае расплава KF-A1F3, парциальные давления компонентов м. б. ниже рассчитанных в соответствии с Р. з. на 5-10 порядков.

Закон сформулирован Ф. Раулем в 1885. м. в. Коробов.


Химическая энциклопедия. — М.: Советская энциклопедия. . 1988.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "РАУЛЯ ЗАКОН" в других словарях:

  • РАУЛЯ ЗАКОН — относительное понижение давления насыщенного пара растворителя над разбавленным раствором равно молярной доле растворенного вещества N:(po p1)/po = N, где po и p1 соответствующее давление насыщенного пара чистого растворителя и растворителя над… …   Большой Энциклопедический словарь

  • РАУЛЯ ЗАКОН — зависимость относительного понижения давления парциального пара растворителя от концентрации растворённости вещества. Установлен Ф. Раулем (F. Baoult, 1886) для разбавленных растворов. Согласно Р. з., где р и р1 давление насыщенного пара… …   Физическая энциклопедия

  • РАУЛЯ ЗАКОН — РАУЛЯ ЗАКОН, относительное понижение давления насыщенного пара растворителя над разбавленным раствором равно молярной доле растворенного вещества N:(po p1)/po = N, где po и p1 соответствующее давление насыщенного пара чистого растворителя и… …   Энциклопедический словарь

  • Рауля закон{:} — относительное понижение давления насыщенного пара растворителя над разбавленным раствором равно молярной доле растворённого вещества N: (р0 р1)/р0 = N, где р0 и р1  соответственно давление насыщенного пара чистого растворителя и растворителя над… …   Энциклопедический словарь

  • РАУЛЯ ЗАКОН — относит. понижение давления насыщ. пара растворителя над разбавленным р ром равно молярной доле растворённого в ва N: (< >0 p1)/p> >0 N, где р0 и …   Естествознание. Энциклопедический словарь

  • ЗАКОН РАУЛЯ — (закон упругости пара), гласит, что ДАВЛЕНИЕ НАСЫЩЕННОГО ПАРА в РАСТВОРЕ это сумма результатов умножения значений давления насыщенного пара каждого компонента на мольную долю этого компонента в растворе. (МОЛЬНАЯ доля это отношение количества… …   Научно-технический энциклопедический словарь

  • закон Рауля — (для упругости пара) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN Raoult s law …   Справочник технического переводчика

  • закон дальтона-рауля — Dalton Raoult’s law *Daltonsches und Raoultsches Gesetz – парціальний тиск і го компонента в паровій фазі дорівнює парціальному тиску цього ж компонента в рідинній фазі …   Гірничий енциклопедичний словник

  • закон рауля — Raoult’s peaw *Raoultsches Gesetz – парціальні тиски рі пари кожного з компонентів ідеального розчину при постійній температурі є пропорційними до концентрацій цих компонентів в рідкій фазі хі, виражених в мольних частках: рі = рі хі, де рі… …   Гірничий енциклопедичний словник

  • закон Рауля-Вант-Гоффа — Закон Рауля Вант Гоффа: коллигативные свойства разбавленных растворов изменяются пропорционально количеству растворенного неэлектролита. Общая химия : учебник / А. В. Жолнин [1] …   Химические термины


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»