- Квадратура круга
-
Так называется знаменитая задача: построить квадрат, равновеликий по площади кругу данного радиуса. Эта задача была предметом непрерывного ряда усиленных изысканий греческих математиков и значительно повлияла на поразительные успехи геометрии в древности. Уже давно явилась догадка, что задача К. круга не может быть решена при помощи линейки и циркуля, хотя и не было точных доказательств этого предположения. Ввиду достаточного развития элементарной геометрии Парижская акд. наук в 1775 г., а прочие академии несколько позднее объявили, что они не будут принимать на рассмотрение новые попытки решения К. круга, так как, не принося существенной пользы для науки, подобные изыскания стали бездельно отнимать время и силы исследователей; в настоящее время ни одно ученое учреждение не станет рассматривать претенциозных статей с решением задачи о К. круга, а также задач об удвоении куба и трисекции угла и задачи о вечном движении. После работ Эрмита и Линдемана можно считать доказанною абсолютную невозможность решения К. круга при помощи линейки и циркуля. Ныне этою задачею занимаются только люди, не пошедшие дальше элементарного курса математических наук и которые не вполне ясно понимают, чего, собственно, они добиваются. В большинстве случаев такие люди не знают истории сделанных до сих пор в этой области изысканий и результатов работ выдающихся ученых. Хотя, к сожалению, и теперь еще в книжные магазины поступают брошюры, в которых авторы пытаются решить нерешимую задачу, однако большинство, хотя и смутно, сознает полную невозможность такого решения, и слова "ищет К. круга" являются уже давно синонимом бесплодной траты времени.Площадь круга равна произведению πR2 где π — отношение длины окружности к диаметру (или длина окружности при R = 1, от περιφερεία — окружность), а R — радиус круга. Очевидно, что существует квадрат, площадь которого равновелика площади круга заданного радиуса; сторона такого квадрата должна равняться √(πR). Можно придумать множество геометрических приемов для нахождения стороны этого квадрата, но при нужных к тому построениях придется, кроме прямой линии и круга, употреблять некоторые другие кривые линии и строить особые механические приборы для их вычерчивания. Если говорится, что задача не решается линейною и циркулем, то это никак не означает ее невозможность, а то, что задача не может быть решена следующими двумя операциями (или известным числом повторений этих операций): 1) провести прямую через две заданные точки и продолжить эту прямую сколь угодно далеко в обе стороны (эта операция совершается при помощи линейки) и 2) вычертить круг, если указана некоторая точка, которую должно принять за центр и если радиус круга указан так или иначе отданными раньше построениями или если этот радиус по условию построения можно взять произвольным. Эта операция совершается циркулем. В элементарной геометрии под решением задачи построением разумеется определение точки или линии при помощи последовательного ряда повторений указанных двух операций. Некоторые задачи могут быть решены и одною линейкою, как, напр., построение касательной к кругу из данной внешней точки (см. Полюсы и Поляры); без сомнения, нелепо будет предположение, что и все задачи должны решаться одною линейкою. Точно так же нелепо предположение, что все задачи должны решаться только линейкою и циркулем. Математические рассуждения, которые привели к полному и строгому доказательству невозможности решения некоторых задач при помощи только линейки и циркуля, основываются на следующих соображениях. Свойства прямой линии и круга, как показывается в аналитической геометрии, состоят в том, что какое бы ни было задано построение прямых и кругов, все точки пересечений таких линий дают отрезки, длины которых вычисляются из ряда уравнений первой степени или квадратных, так что подобные построения могут дать лишь такие отрезки, для вычисления длины которых нет надобности выходить из области уравнений первой и второй степеней. Задача К. круга потому невозможна при помощи только линейки и циркуля, что в этом случае приходится строить число √π; что же касается числа π, следовательно, и квадратного корня из него, то это число, как показывают безусловно верные, а в последнее время даже очень просто доказанные теоремы, есть трансцендентное число, т. е. такое, которое не может удовлетворять никакому алгебраическому уравнению какой бы то ни было степени с целыми коэффициентами, т. е. уравнению вида:А0xn + A1xn-1 + A2xn-2 +..... + An-1x + An = 0где все коэффициенты А0, A1... числа целые. Если бы задача К. круга решалась линейкою и циркулем, то число √π, следовательно, и само и строились бы при помощи последовательного и конечного ряда прямых и кругов, а потому число π можно было бы вычислить при помощи ряда уравнений первой степени и квадратных. Из алгебры известно, что какой бы ни был задан ряд уравнений первой и второй степеней и таких, что коэффициенты каждого следующего уравнения зависят от корней предыдущих, всегда можно этот ряд уравнений заменить одним, более высокой степени, с целыми коэффициентами, а потому число π было бы корнем алгебраического уравнения, что невозможно. Из рассмотрения формулы x = √(πR) ясно, что К. круга была бы найдена, если и помимо чисто геометрического построения удалось бы точно выразить длину окружности круга в частях радиуса или просто найти число, точно выражающее величину π. Соответственно этим разным постановкам вопроса в истории изысканий К. круга встречаются то чисто геометрические приемы построений, то попытки вычисления величины π. Уже у египетских математиков находятся первые решения задачи, как построить квадрат, равновеликий данному кругу, или определить соотношение между окружностью и ее диаметром. В Британском музее хранится папирус Ринда, написанный Ахмесом за 2000 лет до Р. Хр., в котором автор называет свое решение сводом правил, известных еще гораздо раньше. По Ахмесу, сторона квадрата, равновеликого площади круга, равна восьми девятым диаметра (так что π = 3,16). — У древних вавилонян и евреев принималось, что окружность ровно втрое больше диаметра и, следовательно, π = 3 (см. III Книгу Царств, VIII, 23, и II книгу Паралипоменон, IV, 2). — У греков, по словам Платона, К. круга занимался уже Анаксагор во время своего пребывания в изгнании (V в. до Р. Хр.). Первая попытка указать "пределы" для числа π была сделана Бризоном, который справедливо говорит, что окружность круга должна быть меньше периметра многоугольника, описанного около нее, и больше периметра вписанного в нее многоугольника. Гиппократ старался определить площадь круга при помощи так наз. "луночек". Динострат спрямил окружность при помощи построения особой кривой "квадратриссы" (см. Динострат). Замечательно, что знаменитый Эвклид в своих "Элементах" геометрии совершенно не упоминает о К. круга и рассматривает только отношение площадей кругов разных радиусов. Совершенно самостоятельно и независимо от предшественников взглянул на эту задачу Архимед (об измерении длины окружности — см. Архимед). Он вычислил периметры вписанных и описанных 96-ти угольников и показал, что величина π заключается между пределами 31/7 и 310/71; число 31/7 = 22/7 и до сих пор во многих практических вопросах считается весьма удобным и достаточным приближением для π. Достойно удивления, что свои сложные продолжительные вычисления Архимед производил во времена, когда не употреблялась еще арабская система счисления. Птолемей дал для π число 317/120, более точное, чем 31/7, но оно не вошло в употребление, будучи найдено позднее более простого числа Архимеда. В "Кулвазутрасе", весьма древнем математическом сочинении индусов, находится решение задачи, обратной К. круга: построить круг, равновеликий данному квадрату; по этому решению радиус искомого круга равен половине стороны квадрата, увеличенной на треть разности между половиною диагонали и половиною стороны данного квадрата. Ариабхатта (500 л. по Р. Хр.) вычислил π = 3,1416; это число точнее, чем приближения Архимеда и даже Птолемея, так как вычислитель, следуя методу Архимеда, дошел до 384-угольника. Другой индийский математик, Брамагупта (VII в.), нашел, что π = √10; это число, как связанное с десятичною системою счисления, долгое время считалось лучшим приближением и неизменно употреблялось потом всеми арабскими математиками. В китайских книгах найдена величина π = 37/50, которая менее точна, чем число Архимеда. В Европе изыскания К. круга начались лишь с XV в. Кардинал Николай Куза нашел следующее решение: по данному кругу должно построить другой, диаметр которого равен радиусу данного круга плюс сторона вписанного в него квадрата. Тогда периметр вписанного во второй круг равностороннего треугольника равен окружности данного круга. Легко рассчитать, что это приближение хуже приближения Архимеда. Симон Ван-Эйк в конце XVI в. обнародовал сложное построение, которое дает для π величину более точную, чем приближение Архимеда. Чтобы доказать неверность этого построения, другой голландский математик, Адриан Мециус, занялся изысканием для π величины более точной, чем 22/7. Таким образом, ошибочное построение Ван-Эйка было поводом к открытию знаменитой и легко запоминаемой дроби 355/113, которая представляет отношение окружности к диаметру с точностью до 0,000001. Не лишнее заметить, что ныне при помощи теории непрерывных дробей доказано, что при употреблении только трехзначных чисел никакие два другие числа не могут представить величину π точнее, чем отношение 355:113, найденное Мециусом. Неутомимый вычислитель Романус, применяя способ Архимеда, дошел до многоугольников о 1073741824 сторонах, т. е. числа сторон, равного 230. Но Лудольф Ван-Цейлен превзошел его и для π дал число с 35-ю десятичными знаками. Это число, названное "лудольфовым", равно3,14159265358979323846264338327950288[Для запоминания первых 23-х цифр этого числа существует следующее французское четырехстишье, из которого надо выписывать число букв в каждом слове:Que j'aime à fasre apprendreUn nombre utile aux sages!Illustre Archimède, artiste ingenieurQui de ton jugement peut priser la valeur.].Снеллиус и Гюйгенс в XVII в. указали новые пути, дающие возможность, рассматривая многоугольники с меньшим числом сторон, находить приближения для π гораздо скорее и с большим числом десятичных знаков. Однако вычислительные приемы сделались еще проще с тех пор, как для величины π начали открывать формулы, составленные из бесконечного повторения операций над известными числами. Первая мысль отыскать такие формулы принадлежит Виету; он дал ряд
 по которому и вычислил сам величину π до 4-х десятичных знаков. Валлис дал другое замечательное произведение (см. Валлис), а Грегори и независимо от него Лейбниц открыли ряд: π/4 = 1 — 1/3 + 1/5 — 1/7 + 1/9 — 1/11 +... Оригинальный ряд, откуда получается предыдущий как частный случай, есть arctga = a — 1/3a3 + 1/5a5 — 1/7a7 +..., где а есть тангенс центрального угла в круге, которого радиус равен единице. На основании этого ряда легко составить и такой: π/4 = (a + b + c +.... ) — 1/3(a3 + b3 + c3 +... ) + 1/5(a5 + b5 + c5 +... ) —..., где а, b, с,... суть тангенсы углов, которых сумма равна 45°. Выбрав а, b, с,... малыми, легкими для обработки и удовлетворяющими поставленному условию углами, получаются вообще весьма удобные для вычисления ряды. По этому способу лондонский проф. Мехин в 1706 г. вычислил π с 100 десятичными знаками. Он положил a = b = c = d = 1/5 и е = -1/239, т. е. употребил ряд: π /4 = 4[1/5 — 1/(3∙53) + 1/(5∙53) — 1/(7∙53) +... ] — [1/239 — 1/(3∙2393) + 1/(5∙2395) —... ]. До сих пор это лучшая и удобнейшая формула для приближенного вычисления π. Тем не менее, открывают и новые ряды; так, лорд Брункер представил π в виде непрерывной дроби:
по которому и вычислил сам величину π до 4-х десятичных знаков. Валлис дал другое замечательное произведение (см. Валлис), а Грегори и независимо от него Лейбниц открыли ряд: π/4 = 1 — 1/3 + 1/5 — 1/7 + 1/9 — 1/11 +... Оригинальный ряд, откуда получается предыдущий как частный случай, есть arctga = a — 1/3a3 + 1/5a5 — 1/7a7 +..., где а есть тангенс центрального угла в круге, которого радиус равен единице. На основании этого ряда легко составить и такой: π/4 = (a + b + c +.... ) — 1/3(a3 + b3 + c3 +... ) + 1/5(a5 + b5 + c5 +... ) —..., где а, b, с,... суть тангенсы углов, которых сумма равна 45°. Выбрав а, b, с,... малыми, легкими для обработки и удовлетворяющими поставленному условию углами, получаются вообще весьма удобные для вычисления ряды. По этому способу лондонский проф. Мехин в 1706 г. вычислил π с 100 десятичными знаками. Он положил a = b = c = d = 1/5 и е = -1/239, т. е. употребил ряд: π /4 = 4[1/5 — 1/(3∙53) + 1/(5∙53) — 1/(7∙53) +... ] — [1/239 — 1/(3∙2393) + 1/(5∙2395) —... ]. До сих пор это лучшая и удобнейшая формула для приближенного вычисления π. Тем не менее, открывают и новые ряды; так, лорд Брункер представил π в виде непрерывной дроби: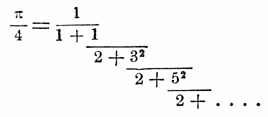 Много строк, бесконечных произведений и непрерывных дробей, дающих π, открыты знаменитым Эйлером, например:
Много строк, бесконечных произведений и непрерывных дробей, дающих π, открыты знаменитым Эйлером, например: По разным подобным формулам современные математики вычисляют величину π с гораздо большею степенью приближения, чем прежние. Дазе нашел 200 цифр, Рихтер 500, а Шанкс даже 700. Однако такое точное вычисление не имеет ни теоретического интереса, ни практического значения. Вообразим шар, которого радиус равен расстоянию Сириуса от Земли (около 134 биллионов километров) и наполненный микробами так тесно, что в каждом кубическом миллиметре их помещается целый биллион (1012). Вообразим далее, что все эти микробы выровнены на прямой и расстояние между каждыми двумя соседними равно расстоянию Сириуса от Земли. Примем теперь эту прямую за диаметр круга и вычислим длину окружности этого круга при помощи π с 100 десятичными знаками. Полученное число даст длину этой окружности с ошибкою против истины лишь в одну миллионную миллиметра. Упомянем еще об одном любопытном приеме для приближенного определения π, основанном на совершенно иных началах. Если начертить на полу систему равноотстоящих параллельных и взаимно перпендикулярных прямых, образующих равные квадратики, и бросать на пол иглу, длина которой равна стороне каждого квадратика, то, считая случаи, когда упавшая игла поместится внутри какого-нибудь квадратика, не пересекая его сторон, получим, что вероятность этого числа, т. е. отношение числа таких попаданий к общему числу бросаний, равна (π — 3). Проф. Вольф в Цюрихе, предложивший этот способ, бросал иглу 10000 раз и получил π с тремя верными десятичными знаками. В заключение перечислим ученых, которым наука обязана объяснением невозможности К. круга. Ламберт в 1761 г. доказал, что π не есть рациональное число и не есть корень из рационального числа, т. е. что ни π, ни π2 не могут быть представлены простыми дробями, как бы ни были велики их числители и знаменатели. Лежандр первый высказал мысль, что π должно быть число трансцендентное, но только Эрмит в сочинении "Sur la Fonction Exponentielle" ("Comptes Rendus", т. 77, 1873) показал, что основание Неперовых логарифмов, т. е. число е, есть трансцендентное, а Линдеман в 1882 г. ("Mathematische Annalen", т. XX), на основании соображений, подобных соображениям Эрмита, показал, что и π есть число трансцендентное. Теорема Линдемана заключается в том, что если х есть корень алгебраического уравнения, которого коэффициенты действительные или мнимые числа, то еx не может быть числом алгебраическим; а так как
По разным подобным формулам современные математики вычисляют величину π с гораздо большею степенью приближения, чем прежние. Дазе нашел 200 цифр, Рихтер 500, а Шанкс даже 700. Однако такое точное вычисление не имеет ни теоретического интереса, ни практического значения. Вообразим шар, которого радиус равен расстоянию Сириуса от Земли (около 134 биллионов километров) и наполненный микробами так тесно, что в каждом кубическом миллиметре их помещается целый биллион (1012). Вообразим далее, что все эти микробы выровнены на прямой и расстояние между каждыми двумя соседними равно расстоянию Сириуса от Земли. Примем теперь эту прямую за диаметр круга и вычислим длину окружности этого круга при помощи π с 100 десятичными знаками. Полученное число даст длину этой окружности с ошибкою против истины лишь в одну миллионную миллиметра. Упомянем еще об одном любопытном приеме для приближенного определения π, основанном на совершенно иных началах. Если начертить на полу систему равноотстоящих параллельных и взаимно перпендикулярных прямых, образующих равные квадратики, и бросать на пол иглу, длина которой равна стороне каждого квадратика, то, считая случаи, когда упавшая игла поместится внутри какого-нибудь квадратика, не пересекая его сторон, получим, что вероятность этого числа, т. е. отношение числа таких попаданий к общему числу бросаний, равна (π — 3). Проф. Вольф в Цюрихе, предложивший этот способ, бросал иглу 10000 раз и получил π с тремя верными десятичными знаками. В заключение перечислим ученых, которым наука обязана объяснением невозможности К. круга. Ламберт в 1761 г. доказал, что π не есть рациональное число и не есть корень из рационального числа, т. е. что ни π, ни π2 не могут быть представлены простыми дробями, как бы ни были велики их числители и знаменатели. Лежандр первый высказал мысль, что π должно быть число трансцендентное, но только Эрмит в сочинении "Sur la Fonction Exponentielle" ("Comptes Rendus", т. 77, 1873) показал, что основание Неперовых логарифмов, т. е. число е, есть трансцендентное, а Линдеман в 1882 г. ("Mathematische Annalen", т. XX), на основании соображений, подобных соображениям Эрмита, показал, что и π есть число трансцендентное. Теорема Линдемана заключается в том, что если х есть корень алгебраического уравнения, которого коэффициенты действительные или мнимые числа, то еx не может быть числом алгебраическим; а так как , то, следовательно,
, то, следовательно, 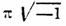 , а потому и π не может быть числом алгебраическим.Литература, Montucla, "Histoire des recherches sur la quadrature du cercle" (Пар., 1754); Rudio, "Vier Abhandlungen über die Kreismessung" (Лпц., 1892); Hurwitz, "Beweis der Trauscendenz der Zahle e und π". На русском языке: Марков, "Доказательство трансцендентности чисел е и π" (СПб., 1883) и перевод статьи Вейерштрасса о невозможности К. круга в "Известиях Физ.-мат. общества при Казанском унив." (1894, № 13).В. Витковский.
, а потому и π не может быть числом алгебраическим.Литература, Montucla, "Histoire des recherches sur la quadrature du cercle" (Пар., 1754); Rudio, "Vier Abhandlungen über die Kreismessung" (Лпц., 1892); Hurwitz, "Beweis der Trauscendenz der Zahle e und π". На русском языке: Марков, "Доказательство трансцендентности чисел е и π" (СПб., 1883) и перевод статьи Вейерштрасса о невозможности К. круга в "Известиях Физ.-мат. общества при Казанском унив." (1894, № 13).В. Витковский.
Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона. — С.-Пб.: Брокгауз-Ефрон. 1890—1907.
