Бойля-Мариотта закон

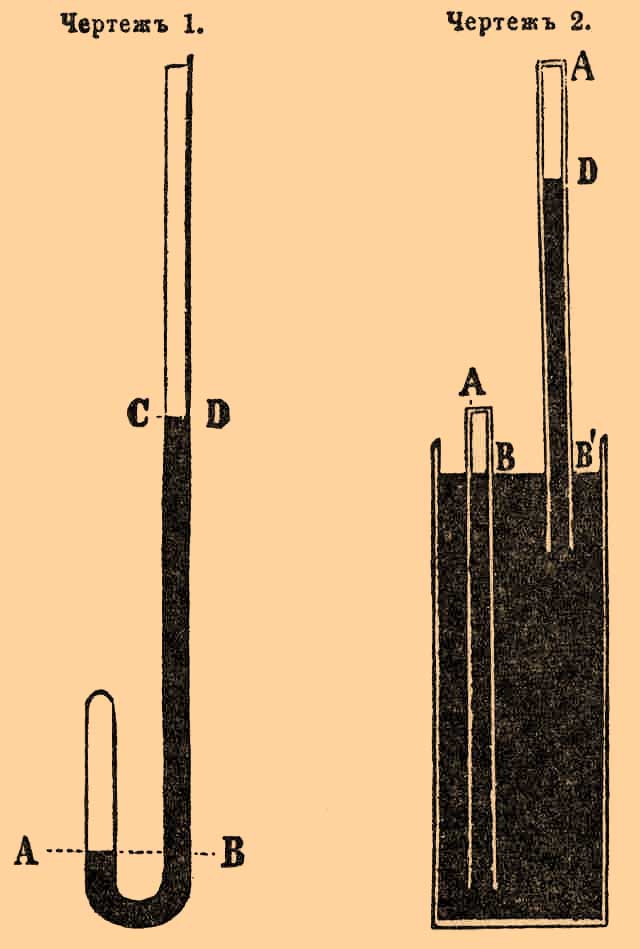
закон, связывающий изменения объема газа при постоянной температуре с изменениями его упругости. Этот закон, открытый в 1660 г. англ. физиком Бойлем и позже, но, независимо от него, Мариоттом во Франции, по своей простоте и определенности занимает весьма важное место в науке, хотя позднейшие исследования показали существование отступлений от него и что закон относится собственно к так называемому идеальному газу. История открытия его весьма поучительна. Франциск Лин (Franciscus Linus), профессор математики в Люттихе (1595—1675), не признавал, чтобы воздух, столь подвижное и легкое вещество, мог поддерживать ртутный столб в барометрической трубке, хотя ученик Галилея Евангелиста Торричелли (1608—1647) несомненно доказал, что именно давление атмосферы есть причина этого явления. До того времени все допускали, что природа не терпит пустоты (horror vacui) и что поэтому в пустые трубки устремляется ртуть, вода и вообще всякие жидкости. Когда же оказалось, что вода в трубке следует за поршнем насоса только до высоты несколько более 30 футов, то Галилей положил, что боязнь пустоты имеет предел. Лин же объяснял, что ртуть держится в трубке невидимыми нитями (funiculus) и что он сам чувствовал эти нити, когда закрывал пальцем верхнее отверстие трубки, которая была потом наполнена ртутью и опрокинута нижним концом в чашечку со ртутью же; при этом ртуть в достаточно длинной трубке опускалась, но останавливалась на известной высоте. Такое толкование опыта Торричелли Лином побудило Бойля сделать несколько новых опытов, которые им описаны в его "A defense of the doctrine touching spring and weight of the air" (Лондон, 1662). Чтобы доказать, что воздух обладает способностью сопротивления, Бойль взял сифонообразную трубку, запаянную на коротком конце (черт. 1).

Когда в длинное колено наливали ртуть, то она сжимала воздух, заключенный в коротком колене, тем значительнее, чем более налито было ртути в другом. Когда ртуть в коротком колене доходила до уровня AB, в длинном она была на уровне CD, значит, упругость сжатого воздуха была такова, что он мог поддерживать давление ртутного столба высотою от AB до CD. А так как эта высота в первых опытах Б. была равна высоте ртути в барометре, то этим доказывалось, что в барометре ртутный столб поддерживался атмосферным воздухом. Наливая различные, все большие и большие количества ртути в длинное колено трубки, Б. записывал высоты ртутного столба и соответственные объемы сжатого воздуха, но сначала не обратил внимания на численные их соотношения. Его ученик Ричард Тоунлей (Richard Townley), просматривая числа таблицы, заметил, что объемы запертого воздуха обратно пропорциональны давлениям, на него производимым. Если воздух занимал сначала 12 дюймов длины в трубке, причем ртуть в обоих коленах была на одной высоте, то когда в длинное колено было прилито столько ртути, что воздух занял только 6 дюймов длины, оказалось, что высота поддерживаемого столба ртути была 29 англ. дюймов. Вначале воздух, запертый в коротком колене, имел упругость одинаковую с атмосферой, которая могла поддерживать в барометре ртуть на 29 дюймов высоты, а во втором случае запертый воздух подвержен был давлению атмосферы и давлению ртутного столба в 29 дюйм., т. е. в сумме — давлению 29 x 2 дюйма: значит, когда объем воздуха стал вдвое меньше, его упругость сделалась вдвое больше. После этого Бойль многократно повторял и разнообразил опыты и доказал, что тот же закон приложим к случаям увеличения объема воздуха.

Для этого он пользовался цилиндрическим сосудом (черт. 2), который был наполнен ртутью; погружая туда трубку А с открытыми концами до тех пор, пока над ртутью оставалась часть AB, длиною равная 1 дюйму, Б. закрывал и заклеивал отверстие А и затем поднимал трубку. При этом объем AB увеличивался и наконец обращался в объем AD — вдвое больший; ртуть же поднималась на высоту B'D, которая была почти вдвое менее, 29¾ дюйма, тогдашней высоты ртути в барометре. Очевидно, что воздух, заключавшийся в DA, не имел достаточной упругости, чтобы давить на поверхность D с такою силою, как он прежде давил на В; разность упругостей в обоих положениях трубки имеет мерою столб DB', которого длина оказалась 15⅜ дюйма. Поэтому упругость воздуха в удвоенном объеме AD составляет 29¾ без 15⅜, т. е. 14⅜ или почти ровно половину прежней. Когда трубка была поднята настолько, что объем AD занял длину в 10 дюймов, то высота ртути DB' оказалась в 26¾, следовательно, упругость воздуха измерялась разностью 29¾ — 26¾, т. е. 3 дюйма, что составляет почти точно 1/10 первоначальной упругости. Описание этих опытов находится в "New Experiments touching the spring of the air" (Оксф., 1660); "Continuation of Experiments" (Оксф., 1669), "On the rarefaction of air" (Лондон, 1671); "Second continuation" (Лондон, 1681), "General history of the air" (Лондон, 1692). Французский ученый Мариотт (Edme Mariotte, 1620—1684) произвел ряд опытов совершенно таким же образом и нашел тот же закон, который обыкновенно и называется его именем; только англичане называют его законом Бойля. См. сочинения Мариотта: "Essay sur la nature de l'Air" (Париж, 1676), "Du mouvement des eaux et des autres fluides" (part. II, disc. 2). Знал ли Мариотт об опытах Бойля — на это положительного ответа нельзя дать, хотя известно, что Мариотт находился в сношениях с английскими учеными уже в 1668 году. Как бы то ни было, Мариотт произвел такие же опыты и измерения, как и Бойль, только с большею точностью, и его опыты сделались более известны. Трубка (черт. 1) получила, как прибор, название Мариоттовой, и закон назван его именем, хотя с некоторого времени по справедливости его называют законом Бойля-Мариотта; может быть, еще справедливее было бы присоединить имя и Тоунлея. Во всяком случае, Мариотт так известен своими другими трудами, что, несмотря на свидетельство цифр, трудно его подозревать в несамостоятельности работ, приведших ко вторичному открытию важного физического закона. История физики показывает, что очень важные законы, открытые в одной стране, могли долгое время быть неизвестными в другой; так, важный закон, касающийся силы гальванического тока, открытый Омом в Германии, был через несколько лет вторично открыт во Франции физиком Пулье.

С уменьшением объема воздуха вдвое-втрое необходимо увеличивается и плотность его в таком же отношении; температура газа при измерении его объема должна быть постоянною, а иначе охлаждение его или нагревание само по себе может изменить объем и упругость; кроме того, воздух не должен содержать воды или иных жидкостей. С соблюдением всех этих условий закон Бойля-Мариотта должен быть выражен таким образом: объемы некоторого определенного количества сухого воздуха при постоянной температуре обратно пропорциональны давлениям, на него производимым, а следовательно, и упругостям его, плотность же воздуха прямо пропорциональна этому давлению; или, вкратце, объем воздуха обратно пропорционален давлению, на него производимому. Если обозначить начальный объем газа буквою v, а давление, под которым он находится, — буквою р, если сжатый объем газа будет v', а давление, всегда измеряемое высотою ртутного столба, будет р'; то закон Б.-М. выразится пропорцией: v : v' = р':р; откуда pv = p'v', т. е. произведение объема газа на соответственное давление есть величина постоянная при не изменяющейся температуре. Другие газы, как будет объяснено далее, следуют тому же закону. Как ни просты кажутся опыты Бойля и Мариотта, однако и при той малой степени точности устройства приборов, какая была доступна в то время, они требовали соблюдения многих экспериментальных предосторожностей. Несоблюдение надлежащих правил было, вероятно, причиною различных разноречивых показаний позднейших наблюдателей. Например, Без наблюдал под экватором в своих опытах уменьшение объема воздуха в меньшем отношении, чем увеличение его упругости. Многочисленные опыты Бугара в тех же широтах, напротив, подтверждали закон Б.-М.; кроме того, опыты Амонтона, Сгравезанда, Фонтаны, Шукбурга привели к тому же заключению.

Но все опыты того времени не доходили до больших давлений и не были так точны, чтобы не оставалось сомнений в верности закона. Зульцер ("Mém. de Berlin", т. IX, 1753), а потом и Робизон заключили из своих опытов, что при давлениях, в 7 или 8 раз превосходивших атмосферное, упругость увеличивается в значительно меньшем отношении, чем уменьшается объем; но опыты Винклера (1765) опять доказывают приложимость закона Б.-М. до 8 атмос. давления. В нынешнем столетии (1826) датские ученые Эрстедт со Свенсеном еще раз подтвердили верность закона до 8 атм. давления; другие их опыты, простиравшиеся до 70 атмосф., сделаны по методе, менее заслуживающей доверия. Но и в этих недалеких пределах (до 8 атм) некоторые газы не следуют закону Б.-М. Во второй половине XVIII стол. Ван Марум удостоверился, что аммиачный газ уменьшается в объеме гораздо быстрее воздуха; подобное тому Эрстедт и Свендсен гораздо позже нашли для газа сернистой кислоты. Вдобавок было открыто, что и тот и другой газы при несколько большем давлении переходят в жидкое состояние; это свойство потом было доказано и для других газов. Депре (Despretz) еще более точными опытами ("Ann. de Chim. et de phys.", 2, XXXIV, 1827) убедился, что очень многие газы не следуют закону Б.-М. даже при таких давлениях, которые далеки от тех, при которых происходит сжижение газов. Депре делал опыты по способу, сходному с употребленным впервые Ван Марумом. Две стеклянные, с одного конца запаянные трубки, из которых одна была наполнена воздухом, а другая иным газом, были погружены открытыми концами в наполненную ртутью ванночку, помещенную на дне стеклянного цилиндра, наполненного водою. Давление производилось на воду посредством поршня, помещенного в верхнем дне цилиндра, вода давила на ртуть, которая, входя в трубочки, сжимала газы. Опыты, сделанные таким прибором, привели Депре к заключению, что аммиачный, сернистый, сероводородный и синеродистый газы при одинаковой величине давления занимают меньший объем, чем воздух. Точность измерений была настолько велика, что разность между сжатием этих газов и воздуха была заметна уже при уменьшении объема последнего только вдвое; при этом объемы названных газов составляли менее половины начального объема. По опытам Депре, водородный газ сжимается одинаково с воздухом до 1/15 первоначального объема, но при двадцати атмосферах давления объем водорода был более соответственного объема воздуха. Дюлонг и Араго ("Mémoires de l'Académie des Sciences", т. X, "Annales de Chim. et de Phys.", т. XLIII, 1830) измеряли сжатие воздуха до 27 атмосфер давления; их прибор состоял из трубки длиною в 1,7 м, в которой был сжимаем воздух, и соединенной с ней другой, составленной из 13 частей, каждая в 2 метра длины. Эта длинная составная трубка была прикреплена к деревянной мачте, установленной внутри высокой башни. Дюлонг и Араго нашли, что закон Б.-М. верен для воздуха даже при сжатии его до 1/24 первоначального объема. Позже французский физик Пулье делал опыты по способу, сходному с тем, которым пользовались Эрстедт и Депре, но при больших давлениях, и заключил, что кислород, азот, водород, окись углерода и окись азота следуют до 100 атмосфер тому же закону сжатия, как и воздух, но что шесть нижепоименованных газов сжимаются более воздуха и что разность между их объемами и объемом воздуха растет с увеличением давления. Эти газы суть: сернистая кислота, аммиак, углекислота, закись азота, маслородный и болотный газы.

В 1847 г. были опубликованы ("Mémoires de l'Académie des sciences de Paris", XXI, 1847) обширные и точные исследования Реньо по этому предмету, которые вместе с прочими физическими работами, исполненными по поручению французского правительства, описаны в указанных мемуарах под заглавием "Relation des expériences entreprises par ordre de M. le ministre des travaux publics etc". Воспользовавшись усовершенствованиями в приборах и способах наблюдения, введенными его предшественниками, Реньо прибавил новые существенные улучшения, устранив главное затруднение в точности измерения постепенно уменьшающихся объемов газа. Как ни значительна была длина трубки, в которой сжимался газ в опытах Араго и Дюлонга (1,7 метра), все же при сильных давлениях объем газа становился очень малым, и тогда всякая маленькая неточность в измерении положения ртути, запирающей газ, становится все более и более ощутительною относительно измеряемого постоянно уменьшающегося объема. Реньо употребил в своих опытах трубку в 3 метра длины для сжатия газов и после измерения полного объема газа и потом сжатого до половины объема при некотором соответственном давлении снова накачивал в эту трубку газ до совершенного ее наполнения. Полученный таким образом опять большой объем газа, находившийся под давлением, большим первоначального, был приводим опять к половинному объему посредством увеличения высоты ртутного столба в длинной трубке. Пользуясь этим способом, Реньо при весьма больших давлениях (для 25 атмосфер для воздуха) измерял всегда большие объемы; кроме того, он принял во внимание много других экспериментальных предосторожностей, обеспечивших ему точность заключений. Опытами Реньо доказано, что важный закон природы, указанный Бойлем и Мариоттом, не формулируется математически точно теми простыми отношениями, которые они дали ему, что сжатие или уменьшение объема воздуха и азота происходит в несколько большем отношении, чем увеличение давления на газ или чем упругости последнего, и что для водорода сжатие, напротив, несколько слабее, чем бы следовало ожидать в случае точной применимости к нему закона Б.-М. Несколько чисел, взятых из мемуаров Реньо, помещенных в следующей табличке, показывают, что замеченные отступления вообще малы, но явно возрастают с увеличением давления. В первых двух столбцах таблицы показаны высоты давящего на газ ртутного столба, выраженные в атмосферах (у Реньо в миллиметрах), причем мерою нормального давления атмосферы принимается высота в 760 млн. ртутного столба. Цифры третьего столбца показывают частные, полученные от разделения отношения первоначального объема газа к объему, уменьшенному сжатием, на отношение последнего давления к первоначальному. Если назвать буквами v, v₁ объемы газа первоначальный и уменьшенный, а букв. р и р₁ — соответственные давления на газ, то по закону Б.-М. должно быть: v : v₁ = р₁ : р, отсюда (v : v₁) : (р₁ : р) = 1, т. е., если оба написанные отношения действительно равны, то частное от разделения одного отношения на другое должно быть равно 1. Но цифры третьего столбца все больше 1 и медленно, но постоянно возрастают:

------------------------------------------------------------------------------------

| A) число атм. давления       |                                      |

|--------------------------------------------| Частное (v : v₁)/(р₁ : р)   |

| начальн. р    | оконч. р₁       |                                      |

|-----------------------------------------------------------------------------------|

| 0,9720           | 1,9411           | 1,001414                       |

|-----------------------------------------------------------------------------------|

| 2,7796           | 5,5888           | 1,002765                       |

|-----------------------------------------------------------------------------------|

| 5,5513           | 11,0580         | 1,003336                       |

|-----------------------------------------------------------------------------------|

| 12,2840         | 24,4092         | 1,006366                       |

------------------------------------------------------------------------------------

Всякое число третьего столбца показывает частное, относящееся к уменьшению объема воздуха вдвое при переходе давления от р (число первого столбца) к р₁ (втор. столб.). Из этих чисел видно, что уменьшение объема воздуха происходит в большем отношении, чем возрастание соответственного давления или упругости газа. Сначала оба отношения мало отличаются между собою, но при переходе от 12 атм. к 24 уменьшение объема в 1,006366 раз значительнее увеличения давления. Небольшое вычисление позволяет заключить, что 10000 куб. сант. воздуха при давлении в 0,972 атм, будучи подвергнуты давлению в 24,9 раз большему, займут объем в 396 куб. сант. вместо 401 к. с., как бы то следовало, если б закон Б.-М. точным образом выражал закон природы.

Сжатие азота представляет подобные же, но несколько меньшие отступления от закона Б.-М., а так как атмосферный воздух состоит из кислорода и азота, то Реньо заключил, что кислород сжимается более, чем азот и воздух. Следующая табличка содержит в себе числа, полученные при опытах I с водородом; цифры столбцов имеют то же значение, как и в таблице А.

B)

----------------------------------------------------------

| 2,9095        | 5,8305        | 0,998584   |

|---------------------------------------------------------|

| близко те же давления  | 0,999373    |

|---------------------------------------------------------|

| 7,6910        | 15,4372      | 0,996121   |

|---------------------------------------------------------|

| 12,0741      | 24,3144      | 0,993335   |

----------------------------------------------------------

Так как все числа третьего столбца меньше единицы и постоянно уменьшаются, то объем сжатого водорода постоянно более, чем бы то следовало по закону Б.-М., и с увеличением давления это отступление возрастает. По уподоблению Реньо, водород сжимается как пружина, все меньше и меньше с возрастанием давления. Что же касается углекислого газа, сравнительно легко сжимающегося, который представляет, подобно воздуху, более быстрое уменьшение объема, чем увеличение упругости, то он отступает от закона уже при сравнительно слабых давлениях при обыкновенной температуре, но, будучи нагрет до температуры кипения воды (100° Ц.), показывает гораздо меньшие отступления. Если из чрезвычайно точных опытов Реньо и следует заключить, что закон Б.-М. с весьма неощутительными отступлениями применяется только к некоторым газам при давлениях, далеких от точки сжижения, и при значительно высокой температуре, то этими результатами изучение вопроса не исчерпывается. Опыты Бойля и Реньо разделены промежутком времени без малого в 200 лет. Свойства газов изучены во многих отношениях в этот промежуток времени, список сжижающихся газов постоянно увеличивался, а несколько лет тому назад трудами Пикте и Кальете (Cailletet) сделано окончательное обобщение, что с уменьшением объема газов посредством давления и с понижением их температуры все они обращаются в жидкость. Вместе с тем исследования над сжатием газов пополнены другими учеными, которые сжимали газ давлениями, далеко превосходящими 25 и 30 атмосфер, на которых остановился Реньо и его ближайшие предшественники. Было упомянуто выше, что уже Пулье доводил давления до 100 атм., но его опыты не так были расположены, чтобы в них можно было найти ответ на значение закона Б.-М. при высоких давлениях. Такой ответ дают опыты Наттерера, Кальете и Амага для сильных давлений и опыты Д. И. Менделеева — для слабых. Амага установил свой прибор на дне шахты, имевшей около 400 метров (около 190 саж.) глубины. Измерения объема газа на такой глубине и огромной высоты давящего ртутного столба сопровождались такими большими техническими затруднениями, что непосредственно была изучена сжимаемость только азота. Закон сжатия других газов по сравнению с азотом был найден Амага по способу Депре и Пулье. В опытах Амага давление достигало 430¾ атмосферы, причем объем азота уменьшился только в 335¾ раза. Кальете опускал свой прибор в артезианский колодец глубиною в 500 метров (около 230 саж.); высота давящего ртутного столба постепенно была увеличиваема по мере опускания прибора. Трубка, в которой сжимался газ, была внутри вызолочена; ртуть, входя в нее, амальгамировала золото, так что на позолоте оставался след, предел между газом и ртутью, по которому и можно было измерять объем, занятый сжатым газом. Кроме того, Кальете производил опыты над сжиманием воздуха и водорода в особом приборе, в котором давления доводились до 605 атмосфер. Этим опытам предшествовали еще исследования Наттерера (1851—1854), который при помощи особого устройства нагнетательного насоса доводил давление на газ до 2790 атмосфер. Газ был сгущаем в толстостенном стальном сосуде, который был снабжен хорошо сделанным клапаном, постепенно нагружаемым по мере увеличения упругости газа, которая и измерялась весом груза на клапане. По окончании сжатия газа он был перепускаем по частям в другой сосуд определенного объема, где он принимал упругость, равную одной атмосфере, причем определялось последовательное уменьшение упругости сжатого газа, сначала быстрое, потом все более и более замедлявшееся. Числа, полученные при этих измерениях, дали средство определить упругости газов, соответственные его сжатию. Совокупность всех этих опытов по сравнению с опытами Реньо привела к тому заключению, что все газы, за исключением водорода, подвергаются таким изменениям объема v и упругости р, начиная с одной атмосферы, что произведение vp уменьшается, пока давление или упругость не достигнет некоторого предела, и что с дальнейшим увеличением давления это произведение vp увеличивается. В первом периоде газы сжимаются более, чем следует по закону Б.-М., во втором периоде — менее. Пределы, т. е. число атмосфер давления, при котором величина сжатия должна получаться согласно закону Б.-М., показаны различными исследователями не одинаково, но несомненно, что для каждого газа есть особый такой предел; только водород при всех испытанных давлениях сжимается меньше, чем следует по закону Б.-М. Оставалось пополнить эти исследования еще изучением связи между упругостью и объемом газов при давлениях, меньших атмосферного, т. е. в разреженном воздухе; по малоточным опытам Бойля и Мариотта, и для разреженного воздуха их закон верен. Точное исследование закона сжатия разреженных газов сделано Д. И. Менделеевым при сотрудничестве М. Л. Кирпичева (опыты Императорского русского технического общества, "Об упругости газов" Д. Менделеева, часть 1, СПб., 1875, in 4°). Эта работа и другие, к ней соприкасающиеся, были произведены на средства Технического общества; на те же средства было напечатано названное сочинение, в котором описаны приемы и приборы автора для измерения упругости и объемов газов. Опыты были произведены над воздухом, водородом и углекислотою. Ниже помещен один ряд опытов, из которых видны соотношения между объемами весьма разреженного воздуха и его упругостью.

С.)

----------------------------------------------------------

| Давления или упругости | Объемы    |

|---------------------------------------------------------|

| 1) 11,906 миллиметра     | 2075         |

|---------------------------------------------------------|

| 2) 1,557 миллиметра      | 15321       |

|---------------------------------------------------------|

| 3) 0,663 миллиметра      | 29363       |

|---------------------------------------------------------|

| 4) 0,353 миллиметра      | 43280       |

----------------------------------------------------------

Отсюда видно, что с уменьшением давления на газ его объем увеличивается в меньшем отношении, чем уменьшается упругость, следоват., и наоборот: с увеличением давления объем уменьшается в меньшем отношении. В самом деле: второе давление в 7,71 раза менее первого, а второй объем только в 7,38 раза более первого; третье давление в 2,35 раза менее второго, а третий объем в 1,92 раза более второго. Значит, сжатие и расширение воздуха при весьма малых давлениях отступает от закона Б.-М. в ту же сторону, как при весьма сильных давлениях; подобное тому получилось и для углекислоты. По этому же вопросу работали Амага и Зильештром, Реньо тоже сделал несколько измерений с воздухом при упругости в 300 миллим. Реньо и Зильештром пришли к тому заключению, что разреженный воздух отступает от закона Б.-М. в ту же сторону, как и при давлениях несколько выше атмосферного; опыты Амага не привели его к достоверным результатам (см. критическую оценку опытов Р. и З., сделанную Д. И. Менделеевым в сочинении "Об упругости газов", §§ 82, 92, 94.)

Резюмируя все сказанное относительно воздуха, можно видеть, что в разреженном состоянии он сжимается менее, чем следует по закону Б.-М., что при плотности около атмосферной и большей ее воздух сжимается более, чем по закону Б.-М., и, наконец, при весьма большой плотности он опять отступает в ту же сторону, как при весьма малой. При переходе от отступлений в одну сторону к отступлениям в другую воздух необходимо должен сжиматься согласно закону Б.-М., и это происходит всего два раза в пределах от наименьшей исследованной упругости (около ⅓ млн.) до наибольшей (2700 атмосфер). Другие газы, вероятно, следуют тому же закону переменного сжатия, кроме водорода, который постоянно сжимается менее, чем по закону Б.-М.

Давно уже были возбуждены сомнения о том, чтобы газы могли следовать закону Б.-М. при весьма сильных давлениях. Так как при сжатии плотность газа постоянно в такой же мере увеличивается, то можно бы дойти до того, что сжатый газ был бы плотнее самого плотного металла, т. е. что газ, доведенный сжатием до некоторого объема, был бы тяжелее, напр., платины, взятой в том же объеме. Беспредельного уплотнения газа нельзя допустить по той причине, что вещество газа, само по себе занимающее некоторую часть пространства, тем самым поставляет предел сжатию. Новейшая химия (см. Менделеев, "Об упругости газов", стр. 8—12) приводит к соображениям, которые не позволяют допустить, чтобы газ сжатием мог быть доведен до весьма большой плотности. А в действительности замеченный факт, что все испытанные газы при больших давлениях занимают объем не столь малый, как бы следовало по закону Б.-М., и что отступления от этого закона тем значительнее, чем больше давление; этот факт показывает, что уменьшение объема приближается к некоторому пределу. Для некоторых газов при обыкновенной температуре такой предел найден, так как эти газы обращаются в жидкость, а жидкости при самых сильных давлениях лишь весьма незначительно уменьшаются в объеме. Другие газы, не обращающиеся в жидкость от одного сжатия без более или менее значительного понижения температуры, все более и более отступают от закона Б.-М. Водород при 3000 атм. давления занимает объем только в 1000 раз меньший первоначального, т. е. при этом давлении его объем втрое более, чем можно бы ожидать в случае точности закона Б.-М. Несколько опытов Реньо над сжатием газов при температуре кипения воды показывают, что при возвышении температуры отступления от закона Б.-М. становятся менее; это обстоятельство привело его к заключению, что возвышение температуры приближает газ к идеальному состоянию, в котором он следует закону Б.-М., но такое понятие об идеальном газе еще не довольно обосновано. В заключение надо сказать, что закон Б.-М., собственно выражая сжатие газов только в некоторых предельных случаях, тем не менее послужил исходной точкой для изучения их свойств. Вместе с законом Гей-Люссака, относящимся к расширению газов от теплоты, он представляет математическую формулу, которую нужно видоизменить, чтобы представить во всей полноте явления изменения объема газов. Формула Ван дер Вальса (см. это слово) уже глубже проникает в натуру газов.

Несмотря на множество экспериментальных работ над сжатием газов, наука может ожидать еще новых, еще более обширных исследований. Точные и трудные исследования весьма расширенных газов, сделанные Д. И. Менделеевым, ведущие к важным заключениям, желательно бы видеть повторенными и распространенными. Опыты Реньо останутся надолго руководящими, но точность нашего времени может показаться недостаточной в ближайшем будущем.

Ф. Петрушевский.