Ромбическая система

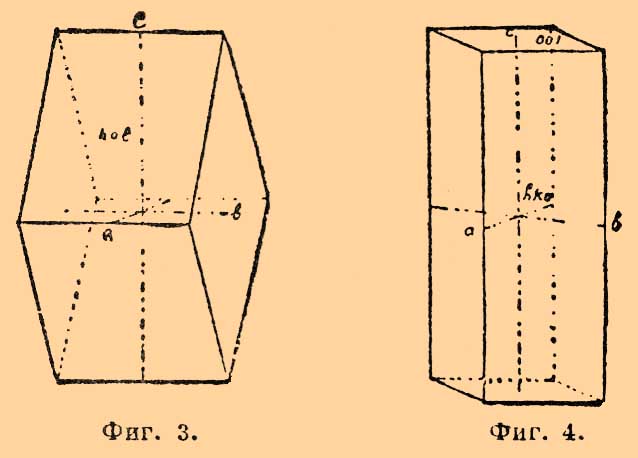
(кристаллограф.) — совокупность естественных многогранников — кристаллов, грани которых могут быть обозначены при помощи трех прямоугольных координатных осей, причем грани, принадлежащие одной простой форме, делают на координатных осях одинаковые отрезки (параметры) и посему могут быть выражены одинаковыми индексами. Если принять отрезки координатных осей плоскостями какой-нибудь формы, принятой за основную, за кристаллические оси, то для Р. системы будет характерно отношение этих осей: a:b:c. Кристаллы, относящиеся к Р. системе, обладают различной степенью симметрии, почему и относятся к трем различным кристаллическим классам:

1) класс ромбической бипирамиды (иначе — голоэдрический или полногранный); характеризуется присутствием центра симметрии (c), трех осей симметрии 2-го порядка (3L²) и трех плоскостей симметрии (3Р). Представителем этого класса служит ромбическая бипирамида — форма, ограниченная восьмью неравносторонними треугольниками и представляющая две пирамиды, сложенные своими ромбическими основаниями (фиг. 1). Общее обозначение этой формы [hkl]. В зависимости от численного значения индексов может быть множество ромбических бипирамид. К этому же классу принадлежат три четырехгранные призматические формы, называемые призмами 1-го, 2-го и 3-го рода, в зависимости от того, параллельно какой из трех кристаллических осей направляются призматические плоскости: a, b или c. Для призмы 1-го рода символ [okl], для призмы 2-го рода [hol] [Призмы 1-го и 2-го рода нередко называются домами: брахи-дома и макро-дома.] и 3-го рода [hk0]. Эти формы изображены на рисунках 2, 3 и 4; как формы открытые, они не могут существовать в природе отдельно, а встречаются в комбинациях с другими формами Р. системы.

Фиг. 1. Фиг. 2

Фиг. 3 и Фиг. 4

Кроме указанных форм, здесь находятся простые формы, состоящие только из двух параллельных плоскостей и называемые пинакоидами. Каждая из плоскостей пинакоидов пересекает только одну какую-нибудь координатную ось, направляясь параллельно двум другим. Смотря по оси, какая пересекается пинакоидом, его называют 1-м, 2-м и 3-м. Символы для пинакоидов — первого [100], второго [010] и третьего [001] [Пинакоиды называются также: макропинакоид, брахипинакоид, базопинакоид.]. Эти пинакоиды изображены на рисунках 2, 3 и 4. Как формы открытые — пинакоиды встречаются только в комбинациях.

2) Класс ромбической пирамиды (гемиморфия). Характеризуется присутствием одной оси симметрии 2-го порядка (L²) и двух плоскостей симметрии (2Р). Представителем служит ромбическая пирамида — форма, ограниченная четырьмя одинаковыми плоскостями, встречающимися в одной точке. Форма открытая; символ [hkl], если плоскости пересекают верхний конец оси с (рис. 5), и [hkĺ] — если пересекают нижний.

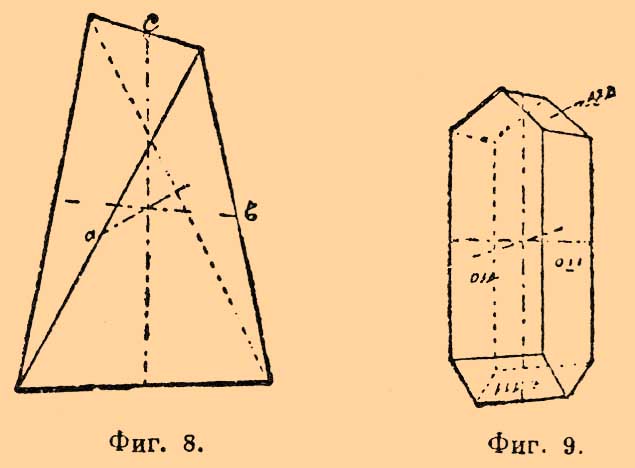
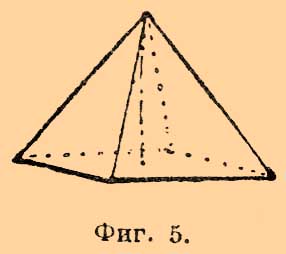Фиг. 5

Сюда относятся: a) формы доматические; каждая состоит из двух плоскостей, пересекающихся в ребре, параллельном или оси a, или оси b; называются: первая — домой первого рода, ее символ [ohl] или [ohĺ] верхняя и нижняя; вторая — домой второго рода, также верхняя и нижняя, ее символ: [hol] и [hoĺ]; b) призмы 3-го рода (как и в первом классе); c) пинакоиды (как и в классе первом) 1-й и 2-й; и d) педионы — простые формы, состоящие только из одной плоскости: верхний педион [001] и нижний педион [001]. Все эти формы открытые и потому встречаются только в комбинациях. Подобная комбинация изображена на рис. 6.

Фиг. 6. Фиг. 7.

3) Класс ромбического бисфеноида или сфеноэдра (гемиэдрия). Характеризуется присутствием трех осей симметрии 2-го порядка (3L²). Представителем служит ромбический бисфеноид или сфеноэдр, форма закрытая, ограниченная четырьмя неравносторонними треугольниками. Символ ромбических бисфеноидов [hkl] и [hќl]. Два бисфеноида, имеющие одинаковые численные значения индексов, но отличающиеся знаками, являются формами энантиоморфными — несовместимыми друг с другом, см. рис. 7 и 8.

Фиг. 8. Фиг. 9.

К тому же классу относятся формы, по наружному виду тождественные с соответствующими формами первого класса, а именно формы призматические — призмы 1-го, 2-го и 3-го рода; пинакоиды — 1-й, 2-й и 3-й. На рис. 9 изображена комбинация некоторых указанных форм (кристалл сернокислой магнезии MgSO₄.7H₂O).

П. З.