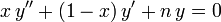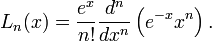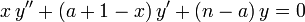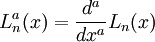Обобщенные полиномы Лагерра

В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834—1886), являются каноническими решениями Уравнения Лагерра:

$x\,y'' + (1 - x)\,y' + n\,y = 0\,$

являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение только в случае, когда n неотрицательно.

Многочлены Лагерра, обычно обозначающиеся как 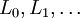$L_0, L_1, \dots$, являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса

$L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}\left(e^{-x} x^n\right).$

Несколько первых многочленов

В следующей таблице приведены несколько первых многочленов Лагерра:

n	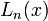$L_n(x)\,$
0	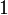$1\,$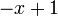
1	$-x+1\,$
2	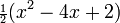${\scriptstyle\frac{1}{2}} (x^2-4x+2) \,$
3	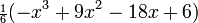${\scriptstyle\frac{1}{6}} (-x^3+9x^2-18x+6) \,$
4	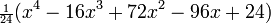${\scriptstyle\frac{1}{24}} (x^4-16x^3+72x^2-96x+24) \,$
5	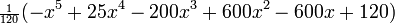${\scriptstyle\frac{1}{120}} (-x^5+25x^4-200x^3+6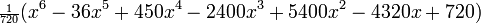00x^2-600x+120) \,$
6	${\scriptstyle\frac{1}{720}} (x^6-36x^5+450x^4-2400x^3+5400x^2-4320x+720) \,$

Обобщённые полиномы Лагерра

Обобщённые полиномы Лагерра имеют вид:

$~L_{n,l}=A_0+A_1r+...+A_{n-1-l}r^{n-l-1}$

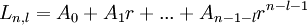
где:

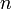• $~n$ — главное (орбитальное) квантовое число;
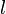• $~l$ — орбитальное (азимутальное) квантовое число.

Обобщённые полиномы Лагерра 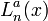$L_n^a(x)$ являются решениями уравнения:

$x\,y'' + (a + 1 - x)\,y' + (n - a)\,y = 0\,$

так что $L_n(x) = L_n^0(x)$.

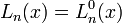Обобщённые полиномы Лагерра могут быть выражены через полиномы Лагерра по формуле:

$L_n^a(x) = \frac{d^a}{dx^a}L_n(x)\,$