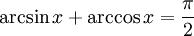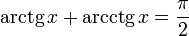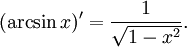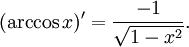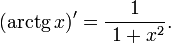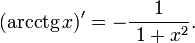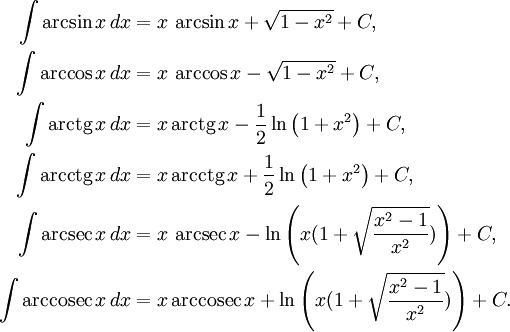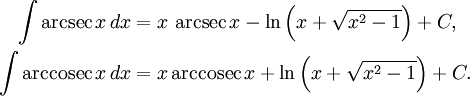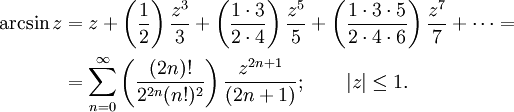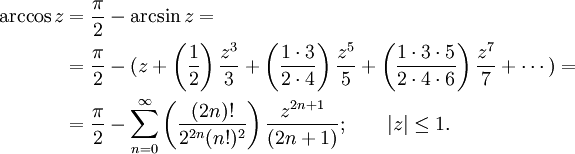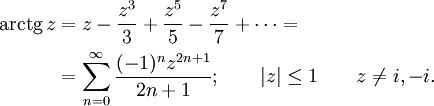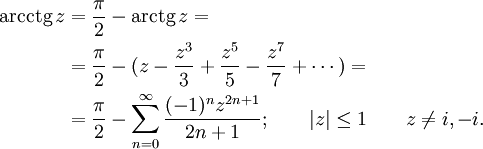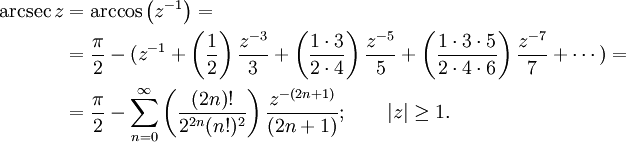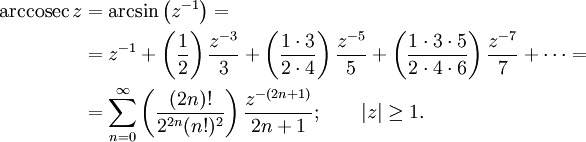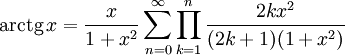- Круговые функции
-
Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т. п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1.
Основное соотношение
Функция arcsin
 График функции y = arcsinx.
График функции y = arcsinx.Арксинусом числа m называется такой угол x, для которого
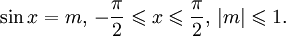
Функция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.
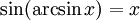 при
при 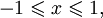
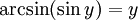 при
при 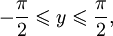
![D(\arcsin x)=[-1; 1]\qquad](/pictures/wiki/files/54/6325ff9dcc6bc9be23bcd886c4dc179c.png) (область определения),
(область определения),![E(\arcsin x) = \left[-\frac{\pi}{2}; \frac{\pi}{2}\right]\qquad](/pictures/wiki/files/52/4986c64f5129adab13f65a88c3d9eda8.png) (область значений).
(область значений).
Свойства функции arcsin
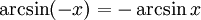 (функция является нечётной).
(функция является нечётной).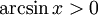 при
при 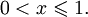
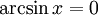 при x = 0.
при x = 0.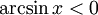 при
при 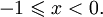
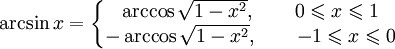
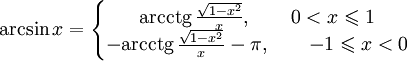
Получение функции arcsin
Дана функция y = sinx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsinx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений —
![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](/pictures/wiki/files/53/5cd520b8b7a376ccf94eb254281f0eb8.png) . Так как для функции y = sinx на интервале
. Так как для функции y = sinx на интервале ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](/pictures/wiki/files/53/5cd520b8b7a376ccf94eb254281f0eb8.png) каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsinx, график которой симметричен графику функции y = sinx на отрезке
каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsinx, график которой симметричен графику функции y = sinx на отрезке ![\left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]](/pictures/wiki/files/53/5cd520b8b7a376ccf94eb254281f0eb8.png) относительно прямой y = x.
относительно прямой y = x.Функция arccos
 График функции y = arccosx.
График функции y = arccosx.Арккосинусом числа m называется такой угол x, для которого
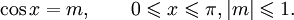
Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.
- cos(arccosx) = x при
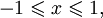
- arccos(cosy) = y при
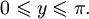
- D(arccosx) = [ − 1;1], (область определения),
- E(arccosx) = [0;π]. (область значений).
Свойства функции arccos
- arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
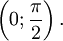
- arccosx > 0 при
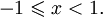
- arccosx = 0 при x = 1.
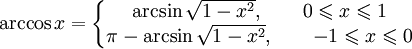
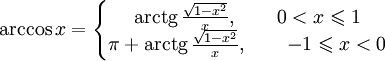
Получение функции arccos
Дана функция y = cosx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccosx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cosx строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccosx, график которой симметричен графику y = cosx на отрезке [0;π] относительно прямой y = x.
Функция arctg
 График функции
График функции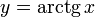 .
.Арктангенсом числа m называется такой угол α, для которого
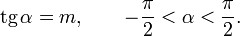
Функция
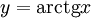 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 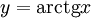 является строго возрастающей.
является строго возрастающей.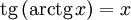 при
при 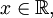
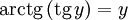 при
при 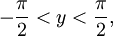
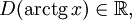
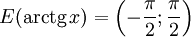
Получение функции arctg
Дана функция
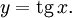 На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 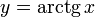 функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —
функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — 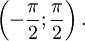 На этом отрезке
На этом отрезке 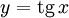 строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале
строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале 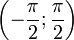 существует обратная
существует обратная 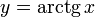 , график которой симметричен графику
, график которой симметричен графику 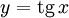 на отрезке
на отрезке 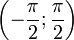 относительно прямой y = x.
относительно прямой y = x.Функция arcctg
 График функции y=arcctg x
График функции y=arcctg xАрккотангенсом числа m называется такой угол x, для которого

Функция
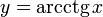 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 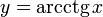 является строго убывающей.
является строго убывающей.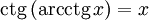 при
при 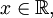
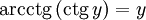 при 0 < y < π,
при 0 < y < π,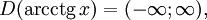
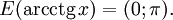
Свойства функции arcctg
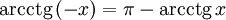 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 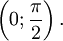
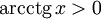 при любых x.
при любых x.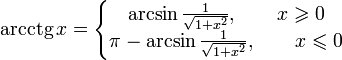
Получение функции arcctg
Дана функция
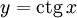 . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 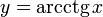 функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке
функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке 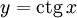 строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция
строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция 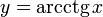 , график которой симметричен графику
, график которой симметричен графику 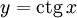 на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу
на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсуФункция arcsec
arcsec(x) = arccos(1/x)
Функция arccosec
arccosec(X) = arcsin(1/x)
Производные от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x≥1:
Разложение в бесконечные ряды
Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:
(член в сумме при n= 0 принимается равным 1).
Использование в геометрии
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.
В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:- α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
См. также
Ссылки
- Weisstein, Eric W. Обратные тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Обратные тригонометрические функции — статья из Большой советской энциклопедии
- Построение графиков обратных тригонометрических функций онлайн
- Онлайн калькулятор: обратные тригонометрические функции
Wikimedia Foundation. 2010.