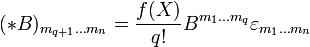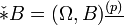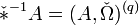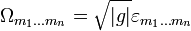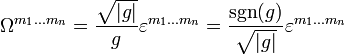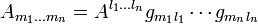- Звёздочка Ходжа
-
Звезда́ Хо́джа — важный линейный оператор из пространства p-векторов в пространство n-p-форм. Метрический тензор задаёт канонический изоморфизм между пространствами p-форм и p-векторов, поэтому обычно звездой Ходжа называют оператор из пространства дифференциальных форм размерности q в пространство форм размерности n-q.
Этот оператор был введён Вильямом Ходжем.
Содержание
Определение
Вспомогательные определения
Определим форму объёма
где
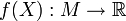 - неотрицательный скаляр на многообразии M, а
- неотрицательный скаляр на многообразии M, а 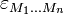 - полностью антисимметричный символ.
- полностью антисимметричный символ. 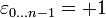 . Даже в отсутствие метрики при f(X)>0 можно определить контравариантые компоненты формы объёма.
. Даже в отсутствие метрики при f(X)>0 можно определить контравариантые компоненты формы объёма.здесь антисимметричный символ
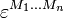 совпадает
совпадает 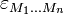 .
.В присутствии метрики Ω с поднятыми индексами может отличаться от
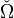 на знак:
на знак: 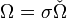 . Здесь и далее σ = sgndet(gmk)
. Здесь и далее σ = sgndet(gmk)Введём операцию антисимметризации:
![A_{[m_1\ldots m_q]}=\frac{1}{q!}\sum_{\sigma(m_1\ldots m_q)}(-1)^{\sgn(m_1\ldots m_q)}A_{\sigma(m_1\ldots m_q)}](/pictures/wiki/files/57/9d41ae180a5c9d824e83d8d6272f4b7a.png) . Суммирование ведётся по всем перестановкам
. Суммирование ведётся по всем перестановкам 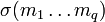 индексов, заключённых в квадратные скобки, с учётом их чётности sgn(σ). Аналогично определяется антисимметризация верхних индексов; антисимметризовать можно только по группе индексов одного типа. Примеры:
индексов, заключённых в квадратные скобки, с учётом их чётности sgn(σ). Аналогично определяется антисимметризация верхних индексов; антисимметризовать можно только по группе индексов одного типа. Примеры: ![A_{k[lm]}=\frac{1}{2!}(A_{klm}-A_{kml})](/pictures/wiki/files/98/b15dc53a1fe094a283d1c1d25a49e468.png) ;
; ![A_k^{[l}B_p^{m]}=\frac{1}{2!}(A_k^l B_p^m - A_k^m B_p^l)](/pictures/wiki/files/48/03a77f44ac3c43afd8ee44f8babb65ce.png) .
.
Определим теперь тензоры:
Индекс (k) указывает число индексов, по которым проводилась свёртка. Там где это не может привести к неоднозначности, (k) будет опускаться. Вышеприведённые тензоры могут отличаться (а могут и не отличаться) только на знак.
Общее определение звезды Ходжа
Используя форму объёма Ω и поливектор
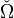 можно ввести операцию * , превращающую поливектор B степени p в дифференциальную форму * B степени n − p, и обратную операцию * − 1, превращающую форму A степени q в поливектор * − 1A степени n − q
можно ввести операцию * , превращающую поливектор B степени p в дифференциальную форму * B степени n − p, и обратную операцию * − 1, превращающую форму A степени q в поливектор * − 1A степени n − q- * B = (Ω,B)(p)
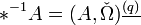
Эта операция называется звездой Ходжа или дуальностью Ходжа. В компонентах она выглядит следующим образом:
Поскольку * − 1 * B = B и * * − 1A = A, то мы установили взаимно-однозначное соответствие между дифференциальными формами степени q и поливекторами степени n-q
Помимо операторов * и * − 1 введём пару операторов:
 и
и 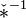 , отличающихся от них знаком.
, отличающихся от них знаком.Звезда Ходжа в присутствии метрики
Пусть на нашем многообразии размерности n задана метрика gmk. Обозначим g = det(gmk).
Элементом объёма или формой объёма порождённой метрикой gmk называется форма
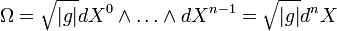 В компонентах:
В компонентах:Поскольку у нас есть метрика, мы можем устроить канонический изоморфизм между поливекторами и дифференциальными формами:
Поэтому мы можем установить взаимно-однозначное соответствие между q-формами и (n-q)-формами.
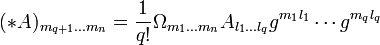
Дополнительные операторы
Свойства звёздочки Ходжа
Источники
- Лекции М.Г.Иванова по курсу "Геометрические методы в классической теории поля". http://theorphys.mipt.ru/courses/geomm.html
Wikimedia Foundation. 2010.

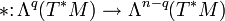
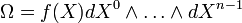
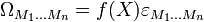
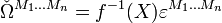
![(A,B)^{(k)}_{M_{k+1}\ldots M_q}{}^{N_{k+1}\ldots N_p}=A_{[ K_1\ldots K_k] M_{k+1}\ldots M_q}{}^{[ K_1\ldots K_k ] N_{k+1}\ldots N_p}](/pictures/wiki/files/57/9a07417f86490c376826982ce932c226.png)
![(A,B)^{\underline{(k)}}_{M_1\ldots M_{q-k}}{}^{N_1\ldots N_{p-k}}=A_{M_1\ldots M_{q-k}[ K_1\ldots K_k ]}{}^{N_1\ldots N_{p-k}[ K_1\ldots K_k ]}](/pictures/wiki/files/57/9230c3aec494bf1609a35df5fbd97a1c.png)