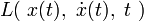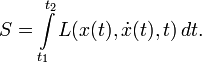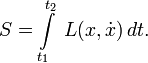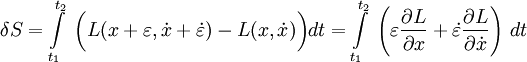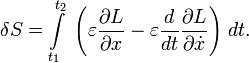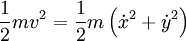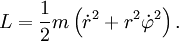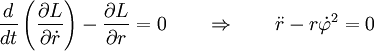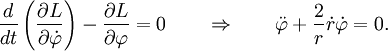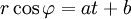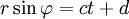Действие (механика)

В физике при́нцип де́йствия является утверждением о природе движения, из которого может быть определена траектория объекта, на который действуют внешние силы. Траектория объекта — та, которая приводит к постоянному значению для физической величины, названной действием. Таким образом, вместо того, чтобы думать об объекте, ускоряющемся в ответ на приложенные силы, можно было думать о силах, которые выделяют траектории со стационарным действием. Принцип также называют принципом стационарного действия и также принцип Гамильтона-Остроградского. Другая формулировка принципа как принцип наименьшего действия менее общая и фактически неправильная.

Действие — скаляр (число) с единицей измерения «Действия» как «Энергия» умножить на «Время». Принцип — простое, общее и мощное средство для того, чтобы предсказать движение в классической механике. Расширения принципа действия описывают релятивистскую механику, квантовую механику, электричество и магнетизм.

Некоторые применения принципа действия

Хотя принцип эквивалентен законам Ньютона в классической механике, но принцип действия лучше подходит для обобщений и играет важную роль в современной физике. Действительно, этот принцип — одно из больших обобщений в физике. В частности, это полностью оценено и лучше всего понято в пределах квантовой механики. Формулировка квантовой механики Ричардом Фейнманом с помощью интегралов по траекториям основана на принципе стационарного действия в качестве классического (т.е. неквантового) предела (иными словами, принцип стационарного действия дает классический предел для фейнмановского интеграла по траекториям). Используя интегралы по траекториям, уравнения Максвелла могут быть получены как условия стационарного действия.

Много проблем в физике могут быть представлены и решены в форме принципа действия, типа обнаружения самого быстрого пути спуска к берегу, чтобы достичь тонущего человека. Текущая вода ищет самый крутой спуск, самый быстрый путь вниз, и вода, сталкивающаяся с бассейном, распределяет себя так, чтобы его поверхность была настолько низка, насколько возможно. Свет находит самый быстрый путь через оптическую систему (принцип Ферма). Траектория тела в поле тяготения (то есть свободное падение в пространстве-времени, так называемая геодезическая) может быть найдена, используя принцип действия.

Симметрии в физической ситуации можно лучше понять, используя принцип действия, вместе с уравнениями Эйлера-Лагранжа, которые получены из принципа действия. Например, теорема Нётер, которая гласит, что каждой непрерывной симметрии в физической ситуации соответствует закон сохранения (верно и обратное). Эта глубокая связь, однако, требует, чтобы принцип действия был принят.

В классической механике правильный выбор действия может быть доказан из законов движения Ньютона. И наоборот, из принципа действия доказываются уравнения движения Ньютона, при правильном выборе действия. Так, в классической механике принцип действия является эквивалентным уравнениям движения Ньютона. Использование принципа действия часто проще, чем прямое решение уравнений движения Ньютона. Принцип действия — скалярная теория, с производными и применениями, которые используют элементарное исчисление.

История

Принцип наименьшего действия был сначала сформулирован Мопертюи [1] в 1746 году и далее развивался (после 1748 года) математиками Эйлером, Лагранжем и Гамильтоном.

Мопертюи пришёл к этому принципу из ощущения, что совершенство вселенной требует определенной экономии в природе и противоречит любым бесполезным расходам энергии. Естественное движение должно быть таким, чтобы сделать некоторую величину минимальной. Нужно было только найти эту величину, что он и продолжал делать. Она являлась произведением продолжительности (время) движения в пределах системы на удвоенную величину, которую мы теперь называем кинетической энергией системы.

Эйлер (в «Reflexions sur quelques loix generales de la nature», 1748) принимает принцип наименьшего количества действия, называя его «усилием». Его выражение соответствует тому, что мы теперь назвали бы потенциальной энергией, так что его утверждение наименьшего количества действия в статике эквивалентно принципу, что система тел в покое примет конфигурацию, которая минимизирует полную потенциальную энергию.

Принцип действия в классической механике

Уравнения движения Ньютона можно получить многими способами, т.е. Ньютонова механика может быть аксиоматически сформулирована по-разному. Один из них с помощью лагранжева формализма, также называемого лагранжевой механикой. Если обозначить траекторию движения частицы, как функцию времени t как x(t), со скоростью 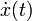$\dot x(t)$, тогда лагранжиан — функция от этих величин и возможно, времени в явном виде:

$L\big(\ x(t),\ \dot{x}(t),\ t\ \big)$

Действие S — интеграл от лагранжиана по времени между заданной начальной точкой x(t₁) в момент времени t₁ и заданной конечной точкой x(t₂) в момент времени t₂

$S=\int\limits_{t_1}^{t_2} L\big( x(t),\dot{x}(t),t \big)\, dt.$

В лагранжевой механике траектория объекта находится при помощи пути, для которого интеграл действия «S» является стационарным (минимум или седловая точка). Интеграл действия — функционал (функция, которая принимает значения на пространстве функций, в этом случае «x» («t»)). Для системы с консервативными силами (силы, которые могут быть описаны в терминах потенциала, как гравитационная сила, в отличие от сил трения) выбор функции Лагранжа в виде: кинетическая энергия минус потенциальная энергия, приводит к правильным законам механики Ньютона (отметим, что сумма кинетической и потенциальной энергии — т.е. комбинация тех же величин со знаком плюс - это полная энергия системы).

То, что действие является скаляром, позволяет легко записать его не только в декартовых, но и в любых других (именуемых в этом смысле обобщенными координатами), главное только, чтобы положение (конфигурация) системы однозначно ими характеризовалось (например, вместо декартовых это могут быть полярные координаты, расстояния межлу точками системы, углы или их функции итд итд). И затем из стационарности действия простыми методами вариационное исчисление автоматически получить уравнения движения в любых обобщенных координатах, в принципе - какими бы сложными они ни были (см.следующий параграф). А это позволяет не только серьезно обобщить формулировку механики, но и выбирать наиболее удобные координаты для каждой определенной задачи, не ограничиваясь декартовыми, что может быть очень полезно для получения наиболее простых и легко решаемых уравнений.

Уравнения Эйлера-Лагранжа для интеграла действия

Стационарная точка интеграла вдоль пути эквивалентна системе дифференциальных уравнений, названных уравнениями Эйлера-Лагранжа. Это может быть замечено следующим образом (ограничимся одномерным случаем). Обобщение на многомерный случай тривиально.

Предположим, имеется интеграл действия S с подинтегральной функцией L, который зависит от координат x(t) и их производных dx(t)/dt, по времени t:

$S = \int\limits_{t_1}^{t_2}\; L(x,\dot{x})\,dt.$

Рассмотрим вторую кривую x₁(t), которая начинается и заканчивается в тех же точках, что и первая кривая, и предположим, что расстояние между двумя кривыми мало: ε(t) = x₁(t) — x(t). В начальной и конечной точках мы имеем ε(t₁) = ε(t₂) = 0.

Разница между интегралами по пути 1 и по пути 2 равна

$\delta S = \int\limits_{t_1}^{t_2}\; \bigg( L(x+\varepsilon,\dot x+\dot\varepsilon)- L(x,\dot x) \bigg)dt = \int\limits_{t_1}^{t_2}\; \left( \varepsilon{\partial L\over\partial x} + \dot\varepsilon{\partial L\over\partial \dot x} \right)\,dt$

где мы использовали разложение L до первого порядка по ε и ε′. Теперь используя интегрирование по частям для последнего слагаемого и используя условия ε(t₁) = ε(t₂) = 0 найдём

$\delta S = \int\limits_{t_1}^{t_2}\; \left( \varepsilon{\partial L\over \partial x} - \varepsilon{d\over dt }{\partial L\over\partial \dot x} \right)\,dt.$

S достигает стационарной точки, то есть δ S = 0 для каждого ε. Заметим, что точка может быть как минимумом, так и седловой точкой, и даже максимумом, если говорить формально. δ S = 0 для каждого ε если и только если

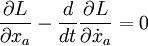${\partial L\over\partial x_{a}} - {d\over dt }{\partial L\over\partial \dot{x}_{a}} = 0$   Уравнения Лагранжа-Эйлера

Где мы заменили x_a, a = 0,1,2,3 на x, поскольку это выполняется для всех координат.

Эта система уравнений называется уравнениями Эйлера-Лагранжа для вариационной задачи. Простое следствие этих уравнений, что если L не зависит явно от x, то есть

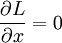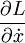если $\frac{\partial L}{\partial x}=0$, то $\frac{\partial L}{\partial\dot x}$ константа.

Тогда координата x называется циклической координатой, и 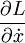$\frac{\partial L}{\partial\dot x}$ называется сопряжённым импульсом, который сохраняется.

Например, если L не зависит явно от времени, то соответствующий интеграл движения (сопряжённый импульс) называется энергией. При использовании сферических координат t, r, φ, θ если L не зависит от φ, сохраняющийся сопряжённый импульс — угловой момент.

Для тех, кто знаком с функциональным анализом заметим, что уравнения упрощаются

$\frac{\delta S}{\delta x_{i}(t)}=0$.

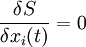Пример: свободная частица в полярных координатах

Тривиальные примеры помогают оценивать использование принципа действия через уравнения Эйлера-Лагранжа. Свободная частица (масса m и скорость v) в Евклидовом пространстве перемещается по прямой линии. Используя уравнения Эйлера-Лагранжа, это можно показать в полярных координатах следующим образом. В отсутствие потенциала функция Лагранжа просто равна кинетической энергии

$\frac{1}{2} mv^2= \frac{1}{2}m \left( \dot{x}^2 + \dot{y}^2 \right)$

в ортогональной системе координат (x, y).

В полярных координатах (r, φ) кинетическая энергия, и следовательно, функция Лагранжа становится

$L = \frac{1}{2}m \left( \dot{r}^2 + r^2\dot\varphi^2 \right).$

Радиальная компонента r и φ' уравнений становятся, соответственно

$\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{r}} \right) - \frac{\partial L}{\partial r} = 0 \qquad \Rightarrow \qquad \ddot{r} - r\dot{\varphi}^2 = 0$

$\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{\varphi}} \right) -\frac{\partial L}{\partial \varphi} = 0 \qquad \Rightarrow \qquad \ddot{\varphi} + \frac{2}{r}\dot{r}\dot{\varphi} = 0.$

Решение этих двух уравнений

$r\cos\varphi = a t + b$

$r\sin\varphi = c t + d$

ряд констант «a, b, c, d» задаётся начальными условиями. Таким образом, действительно, «решение — прямая линия», заданная в полярных координатах.

---

Формализм, приведённый выше, действителен в классической механике в очень ограничительном смысле. Более широко, действие — функционал, задающий отображение из конфигурационного пространства на множество вещественных чисел и, в общем, оно не обязано быть интегралом, потому что нелокальные действия в принципе возможны, по крайней мере, теоретически.

Смотрите также

• Действие (физическая величина)
• Лагранжиан
• Лагранжева механика
• Теорема Нётер
• Гамильтонова механика
• Вариационное исчисление
• Энтропия (У принципа наименьшего действия и принципа максимальной вероятности или энтропии можно рассмотреть аналогии)

Литература на русском языке

• Вариационные принципы механики. Сб. статей классиков науки. Под редакцией Полака Л.С. М.: Физматгиз. 1959.
• Веретенников В. Г., Синицын В. А. Метод переменного действия. 2-ое издание. М.: Физматлит, 2005.
• Гантмахер Ф. Р. Лекции по аналитической механике. 2-е издание М.: Наука, 1966.
• Добронравов В. В. Основы аналитической механики. М.: Высшая школа, 1976.
• Ланцош К. Вариационные принципы механики. М.: Физматгиз. 1965.
• Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
• Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. - 392с.
• Парс Л. А. Аналитическая динамика. М.: Наука, 1971.

Литература

Для библиографии с аннотацией смотрите Edwin F. Taylor [2] Среди библиографического списка есть следующие книги

1. Cornelius Lanczos, The Variational Principles of Mechanics (Dover Publications, New York, 1986). ISBN 0-486-65067-7. Наиболее цитируемый источник в этой области.
2. L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics (Butterworth-Heinenann, 1976), 3rd ed., Vol. 1. ISBN 0-7506-2896-0. Начинается с принципа наименьшего действия.
3. Thomas A. Moore «Least-Action Principle» in Macmillan Encyclopedia of Physics (Simon & Schuster Macmillan, 1996), Volume 2, ISBN 0-0286457-1, pages 840—842.
4. David Morin знакомит с уравнениями Лагранжа в главе 5 его книги. Включает 27 задач с решениями. Черновой вариант доступен [3]
5. Gerald Jay Sussman and Jack Wisdom, Structure and Interpretation of Classical Mechanics (MIT Press, 2001). Начинается с принципа наименьшего действия, использует современные обозначения.
6. Dare A. Wells, Lagrangian Dynamics, Schaum’s Outline Series (McGraw-Hill, 1967) ISBN 0-07-069258-0.
7. Robert Weinstock, Calculus of Variations, with Applications to Physics and Engineering (Dover Publications, 1974). ISBN 0-486-63069-2. Старая добротная книга, где формализм определяется до использования.
8. Stephen Wolfram, A New Kind of Science. May 2002. ISBN 1-57955-008-8.

Внешние ссылки

1. Edwin F. Taylor’s страница [4]
2. Исторические записи:
   1. Статьи Гамильтона в форматах TeX, DVI, PDF, и PostScript доступны [5]
   2. Статьи Гамильтона, посвящённые принципу действия, доступны по адресу [6]