Грань числового множества

Точная верхняя грань и точная нижняя грань — обобщение понятий максимума и минимума множества соответственно.

Определения

Точной верхней гранью, или супре́мумом (лат. supremum — самый высокий) подмножества X упорядоченного множества M, называется наименьший элемент M, который равен или больше всех элементов множества X. Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается $\sup X$.

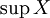Более формально:

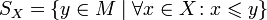$S_X=\{y\in M\mid\forall x\in X\!:x\leqslant y\}\!$ — множество верхних граней X, то есть элементов M, равных или больших всех элементов X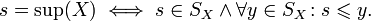

$s=\sup(X)\iff s\in S_X\and\forall y\in S_X\!:s\leqslant y.$

Точной нижней гранью, или и́нфимумом (лат. infimum — самый низкий) подмножества X упорядоченного множества M, называется наибольший элемент M, который равен или меньше всех элементов множества X. Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается $\inf X$.

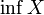Замечание

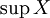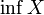Эти определения ничего не говорят о том, принадлежит ли $\sup X$ и $\inf X$ множеству X или нет. В случае 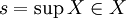$s=\sup X\in X$, говорят, что s является максимумом X. В случае 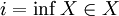$i=\inf X\in X$, говорят, что i является минимумом X.

Примеры

• На множестве всех действительных чисел, больших пяти, не существует минимума, однако существует инфимум. 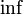$\inf$ такого множества равен пяти. Инфимум не является минимумом, так как пять не принадлежит этому множеству. Если же определить множество всех натуральных чисел, больших пяти, то у такого множества есть минимум и он равен шести. Вообще говоря, у любого подмножества множества натуральных чисел существует минимум^[1].
• Для множества $S=\left\{\frac{1}{k}\mid k\in\Bbb N\right\}=\left\{1,\;\frac{1}{2},\;\frac{1}{3},\;\ldots\right\}$

$\sup S=1$; $\inf S=0$.

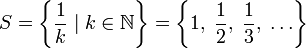
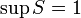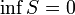• Множество положительных действительных чисел 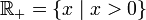$\Bbb R_+=\{x\mid x>0\}$ не имеет точной верхней грани в 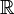$\Bbb R$, точная нижняя грань $\inf\Bbb R_+=0$.
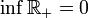• Множество 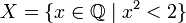$X=\{x\in\Bbb Q\mid x^2<2\}$ рациональных чисел, квадрат которых меньше двух, не имеет точных верхней и нижней граней в 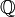$\Bbb Q$, но если его рассматривать как подмножество множества действительных чисел, то

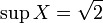$\sup X=\sqrt{2}$ и $\inf X=-\sqrt{2}$.

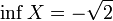Свойства

• Для любого ограниченного сверху подмножества $\mathbb{R}$, существует $\sup$.
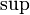• Для любого ограниченного снизу подмножества $\mathbb{R}$, существует $\inf$.
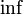• Вещественное число s является 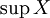$\sup X$ тогда и только тогда
  1. s есть верхняя грань X то есть для всех элементов $x\in X$, $x\leqslant s$.
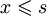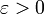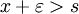  2. для любого $\varepsilon>0$ найдётся $x\in X$, такой, что $x+\varepsilon > s$ (то есть к s можно сколь угодно «близко подобраться» из множества X)
• Аналогичное утверждение верно для точной нижней грани.

Вариации и обобщения

• Существенный супремум

Примечания

1. ↑ Строго говоря, у любого подмножества вполне упорядоченного множества существует в силу принципа фундированности минимум.