- Вещественная переменная
-
Веще́ственные, или действи́тельные[1] числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.
Множество вещественных чисел обозначается
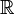 (Unicode: ℝ) и часто называется вещественной прямой.
(Unicode: ℝ) и часто называется вещественной прямой.Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.
Содержание
Примеры
- Рациональные числа — 32, 36/29.
- Иррациональные числа — π,
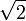 .
.
Определения
Существует несколько стандартных путей определения вещественных чисел:
Аксиоматическое определение
См. основную статью Аксиоматика вещественных чисел.
Множество вещественных чисел
 можно определить как топологически полное, упорядоченное поле, то есть поле с отношением
можно определить как топологически полное, упорядоченное поле, то есть поле с отношением 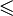 , которое удовлетворяет следующим аксиомам:
, которое удовлетворяет следующим аксиомам:- Отношение
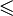 является отношением линейного порядка:
является отношением линейного порядка:
- Для любых
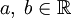
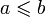 или
или 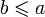 ;
; - Если
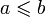 и
и 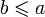 , то a = b для любых
, то a = b для любых 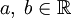 ;
; - Если
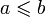 и
и 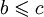 , то
, то 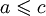 для любых
для любых 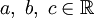 ;
;
- Для любых
- Порядок согласован со структурой поля:
- Если
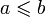 , то
, то 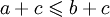 для любых
для любых 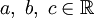 ;
; - Если
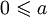 и
и 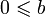 , то
, то 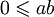 .
.
- Если
- Порядок на
 удовлетворяет условию полноты:
удовлетворяет условию полноты:
- Пусть
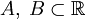 — непустые подмножества, такие что
— непустые подмножества, такие что 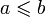 для любых
для любых 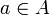 и
и 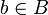 , тогда существует
, тогда существует 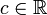 такое, что
такое, что 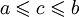 для любых
для любых 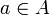 и
и 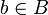 .
.
- Пусть
Примечания
Из свойства 3 следует, что у любого непустого ограниченного сверху множества
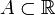 (то есть такого, что для всех x из A все
(то есть такого, что для всех x из A все 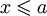 для некоторого
для некоторого 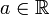 ) существует точная верхняя грань (минимальная из всех), то есть число
) существует точная верхняя грань (минимальная из всех), то есть число 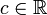 такое, что
такое, что- Для всех x из A все
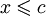
- Если свойству (1) удовлетворяет также число
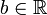 , то
, то 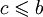 .
.
Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля
 .
.Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)
Пополнение рациональных чисел
Вещественные числа
 могут быть построены как пополнение множества рациональных чисел
могут быть построены как пополнение множества рациональных чисел 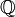 по отношению к обычной метрике
по отношению к обычной метрике 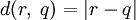 .
.Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {ri}. На таких последовательностях можно естественным образом ввести арифметические операции: {ri} + {qi} = {ri + qi} и
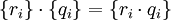 .
.Две такие последовательности
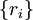 и
и 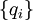 считаются эквивалентными
считаются эквивалентными 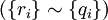 , если
, если 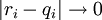 при
при 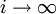 .
.Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.
Дедекиндовы сечения
См. основную статью Дедекиндово сечение.
Дедекиндово сечение — это разбиение множества рациональных чисел
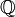 на два подмножества A и B такие, что:
на два подмножества A и B такие, что: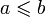 для любых
для любых 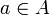 и
и 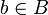 ;
;- B не имеет минимального элемента.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Например, вещественному числу
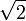 соответствует дедекиндово сечение, определяемое
соответствует дедекиндово сечение, определяемое 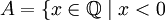 или
или 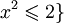 и
и 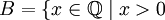 и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить
и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить 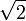 мы рассекли множество на две части: все числа, что левее
мы рассекли множество на две части: все числа, что левее 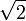 и все числа, что правее
и все числа, что правее 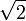 ; соотвеетственно,
; соотвеетственно, 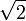 равно точной нижней грани множества B.
равно точной нижней грани множества B.Бесконечные десятичные дроби
Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.
Бесконечной десятичной дробью (со знаком) называется последовательность вида
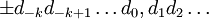 , где di являются десятичными цифрами, то есть
, где di являются десятичными цифрами, то есть 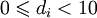 .
.Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид
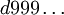 и
и 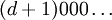 , где
, где 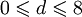 , либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
, либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.
Значение десятичной дроби формально задаётся суммой ряда
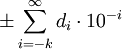 .
.Счетность множества
TODO:
Примечания
Ссылки
- Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
- Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.
См. также
Wikimedia Foundation. 2010.
