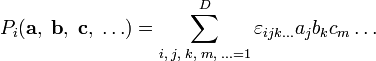- Векторное произведение векторов
-
Содержание
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов
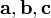 называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.Определение
Векторным произведением вектора
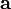 на вектор
на вектор 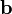 называется вектор
называется вектор 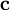 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:- вектор
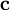 ортогонален каждому из векторов
ортогонален каждому из векторов 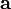 и
и 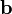
- вектор
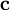 направлен так, что тройка векторов
направлен так, что тройка векторов 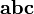 является правой.
является правой.
Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
- Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
- Модуль векторного произведения
![[\mathbf{ab}]](/pictures/wiki/files/48/01897afd149a19972788eb8c4a09e7d5.png) равняется площади S параллелограмма, построенного на приведённых к общему началу векторах
равняется площади S параллелограмма, построенного на приведённых к общему началу векторах 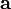 и
и 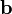
- Если
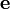 — единичный вектор, ортогональный векторам
— единичный вектор, ортогональный векторам 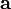 и
и 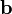 , а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если
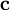 — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор,
— какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, 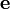 — единичный вектор, лежащий в плоскости π и ортогональный к
— единичный вектор, лежащий в плоскости π и ортогональный к 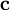 ,
, 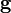 — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов
— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов 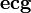 является правой, то для любого лежащего в плоскости π вектора
является правой, то для любого лежащего в плоскости π вектора 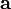 справедлива формула
справедлива формула
Алгебраические свойства векторного произведения
![\left[ \mathbf{a},\; \mathbf b \right] = - \left[ \mathbf b, \mathbf a \right]](/pictures/wiki/files/102/fd1d973e5970611a0799697b0d3deeba.png) (свойство антикоммутативности)
(свойство антикоммутативности)![\left[ \left(\alpha \mathbf a \right),\; \mathbf b \right] = \left[ \mathbf a,\; \left(\alpha \mathbf b \right) \right] = \alpha \left[ \mathbf a,\; \mathbf b \right]](/pictures/wiki/files/50/2d4a74f1abe11e5bbce1da9fc1255ebe.png) (свойство ассоциативности относительно умножения на скаляр)
(свойство ассоциативности относительно умножения на скаляр)![\left[ \left( \mathbf a + \mathbf b \right),\; \mathbf c \right] = \left[ \mathbf a,\; \mathbf c \right] + \left[ \mathbf b,\; \mathbf c \right]](/pictures/wiki/files/53/5970c8ab133c93b1bafe5194c76f55df.png) (свойство дистрибутивности по сложению)
(свойство дистрибутивности по сложению)![\left[ \left[ \mathbf a,\; \mathbf b \right],\; \mathbf c \right] + \left[ \left[ \mathbf b,\; \mathbf c \right],\; \mathbf a \right] + \left[ \left[ \mathbf c, \mathbf a \right],\; \mathbf b \right]= 0](/pictures/wiki/files/55/769ef200b9c11776d1c12cc11f8476a4.png) (тождество Якоби)
(тождество Якоби)![\left[ \mathbf a,\; \mathbf a \right] =\mathbf 0](/pictures/wiki/files/49/1157e2ef3976c54d6016115266277c3f.png)
![\left[ \mathbf a,\; [ \mathbf b,\; \mathbf c ] \right]~=~\mathbf b (\mathbf a,\; \mathbf c) - \mathbf c (\mathbf a,\; \mathbf b)](/pictures/wiki/files/50/219e46cdbab4adc7fe2ec00356bb842b.png) (формула «БАЦ минус ЦАБ», тождество Лагранжа)
(формула «БАЦ минус ЦАБ», тождество Лагранжа)![|[\mathbf a, \, \mathbf b]|^2 + (\mathbf a, \, \mathbf b)^2 = |\mathbf a|^2 |\mathbf b|^2](/pictures/wiki/files/56/859c92b53899eee53db99711a2445533.png) . Это частный случай мультипликативности
. Это частный случай мультипликативности 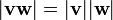 нормы кватернионов
нормы кватернионов![([\mathbf a, \, \mathbf b], \, c)=(\mathbf a, \, [\mathbf b, \, \mathbf c])](/pictures/wiki/files/98/b48a467465050b4c36113eea6d5c18e5.png) ; значение этого выражения называют смешанным произведением векторов a, b, c и обозначают
; значение этого выражения называют смешанным произведением векторов a, b, c и обозначают 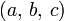 либо
либо 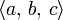 .
.
Выражение для векторного произведения в декартовых координатах
Если два вектора
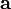 и
и 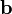 определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисето их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где
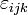 — символ Леви-Чивиты.
— символ Леви-Чивиты.Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы
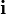 ,
, 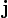 ,
, 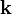 — стандартные обозначения для ортов в
— стандартные обозначения для ортов в 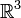 : они рассматриваются как воображаемые кватернионы.
: они рассматриваются как воображаемые кватернионы.Заметим, что соотношения через векторное произведение между
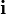 ,
, 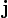 и
и 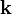 соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор
соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор 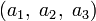 как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть
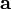 равен векторному произведению:
равен векторному произведению:тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](/pictures/wiki/files/98/b00e919750be3b08a60e4757f3cf9cf9.png) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](/pictures/wiki/files/55/762d1d364c16664eff7d042f99842e70.png)
а так как
![[\mathbf{a}]_{\times}](/pictures/wiki/files/100/d00b55ad4c7fdd0a1f2a424e0ca572ef.png) кососимметрична, то
кососимметрична, тоВ такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица,
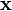 ,
, 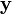 — векторы):
— векторы):После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в
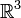 примет вид:
примет вид:где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение
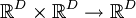 , можно ввести только для размерности 3.
, можно ввести только для размерности 3.Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты
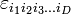 с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение какТакое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
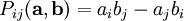 .
.
Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на
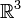 структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам -- антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению
структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам -- антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению 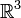 с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.См. также
Произведения векторов
- Косое произведение векторов (2D)
- Скалярное произведение векторов (2D и 3D)
- Смешанное произведение векторов (3D)
- Векторно-векторное произведение векторов (3D)
Другое
Ссылки
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Wikimedia Foundation. 2010.

 ; между ними
; между ними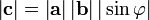
![\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b](/pictures/wiki/files/101/ed09d9154faf68b1a7783004b4cbc46c.png)
![[ \mathbf a,\; \mathbf b ] = S\, \mathbf e](/pictures/wiki/files/50/28395f1def81662c027a8cbd7f6f8aa9.png)
![\left[ \mathbf a,\; \mathbf c \right] = \mathrm{Pr}_{ \mathbf e }\, \mathbf a \left| \mathbf c \right| \mathbf g.](/pictures/wiki/files/48/04002beabcb294e180266aa94180d9b9.png)
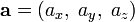
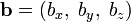
![[ \mathbf a,\; \mathbf b ] = (a_y b_z - a_z b_y,\; a_z b_x - a_x b_z,\; a_x b_y - a_y b_x).](/pictures/wiki/files/52/4c3df91a2cfe53408b07f333a175565a.png)
![[ \mathbf a,\; \mathbf b ] = \begin{vmatrix} \mathbf i &amp; \mathbf j &amp; \mathbf k \\ a_x &amp; a_y &amp; a_z \\ b_x &amp; b_y &amp; b_z \end{vmatrix}](/pictures/wiki/files/49/16ea255c911b3e4c07cc2adae3d7626e.png)
![[ \mathbf a,\; \mathbf b ]_i = \sum_{j,k=1}^3 \varepsilon_{i j k} a_j b_k,](/pictures/wiki/files/55/7c8e6ab7e9c7e3607e920bb75caae299.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,a_2\\ \,\,a_3&amp;0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](/pictures/wiki/files/98/bb0828317b64e54d924e3d9dabb54234.png)
![\mathbf{b} \times \mathbf{a} = \mathbf{b}^T [\mathbf{a}]_{\times} = \begin{bmatrix}b_1&amp;b_2&amp;b_3\end{bmatrix}\begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;\,0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}](/pictures/wiki/files/97/a1999aed4c7add8bb1d9f291beb9a7e9.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;0&amp;\!-a_1\\\!-a_2&amp;\,\,a_1&amp;\,\,0\end{bmatrix}](/pictures/wiki/files/52/42367ea2bfc38aaf3870e9a3aba428bb.png)
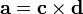
![[\mathbf{a}]_{\times} = (\mathbf{c}\mathbf{d}^T)^T - \mathbf{c}\mathbf{d}^T.](/pictures/wiki/files/53/55d46afc14c256de89aa56b17ef38491.png)
![\mathbf{b}^{T} \, [\mathbf{a}]_{\times} \, \mathbf{b} = 0.](/pictures/wiki/files/98/b0e7a57333b3ebbdf3c81c827152e5fa.png)
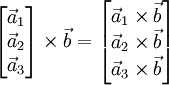
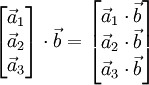
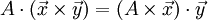
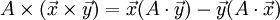
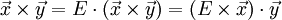
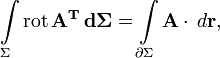
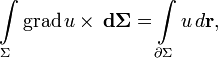
![\int\limits_{\Sigma} \left[ \mathbf{d\Sigma}; \left[ \nabla; \vec a \right] \right] = \int\limits_{\partial\Sigma} \vec a \times d \mathbf{r}.](/pictures/wiki/files/53/552f7432c2a90d787f641f23287017c2.png)