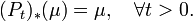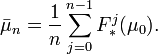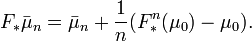- Теорема Крылова — Боголюбова
-
Теорема Крылова — Боголюбова
В теории динамических систем под теоремами Крылова — Боголюбова понимаются две теоремы, утверждающие существование инвариантных мер у «хороших» отображений, определённых на «хороших» пространствах. Теоремы доказаны математиком Н. М. Крыловым и физиком-теоретиком, математиком Н. Н. Боголюбовым.[1][2] (переиздано в [3]).
Содержание
Формулировка теоремы
Инвариантные меры для отображений
Теорема Крылова — Боголюбова для динамических систем утверждает, что
Пусть F — непрерывное отображение метрического компакта X в себя. Тогда на X существует F-инвариантная мера μ.
Стоит отметить, что условие F-инвариантности, F * μ = μ, означает, что мера прообраза любого борелевского множества равна мере этого множества,
при этом в случае необратимого отображения F мера F(A) не обязана равняться мере A. Например, мера Лебега инвариантна для удвоения окружности
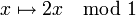 , однако мера дуги [0,1 / 3] не равна мере её образа, дуги [0,2 / 3].
, однако мера дуги [0,1 / 3] не равна мере её образа, дуги [0,2 / 3].Инвариантные меры для марковских процессов
Пусть X — польское пространство и пусть (Pt) — семейство вероятностей перехода некоторой однородной марковской полугруппы на X, т. е.
- Теорема Крылова — Боголюбова утверждает, что если существует
 , для которого семейство вероятностных мер { Pt(x, ·) | t > 0 } uniformly tight и полугруппа (Pt) удовлетворяет Feller property, то существует по крайней мере одна инвариантная мера для (Pt), т. е. такая вероятностная мера μ на X, что
, для которого семейство вероятностных мер { Pt(x, ·) | t > 0 } uniformly tight и полугруппа (Pt) удовлетворяет Feller property, то существует по крайней мере одна инвариантная мера для (Pt), т. е. такая вероятностная мера μ на X, что
Доказательство для динамических систем
Доказательство теоремы опирается на процедуру Крылова-Боголюбова — процедуру выделения сходящейся подпоследовательности из последовательности временных средних произвольной начальной меры.
А именно, берётся произвольная начальная мера μ0, и рассматривается последовательность её временных средних:
Временные средние являются всё более и более F-инвариантными:
Поэтому предел любой сходящейся подпоследовательности последовательности временных средних является инвариантной мерой для отображения F. Но пространство вероятностных мер на метрическом компакте X компактно (в смысле *-слабой топологии), поэтому по меньшей мере одна точка накопления у последовательности
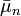 найдётся — что и завершает доказательство.
найдётся — что и завершает доказательство.В случае, если в качестве меры μ0 берётся мера Дирака (сосредоточенная в типичной начальной точке) или мера Лебега, сходимость последовательности
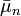 соответствует существованию меры Синая-Рюэлля-Боуэна.
соответствует существованию меры Синая-Рюэлля-Боуэна.Обобщения
Точно такие же рассуждения, только связанные с усреднением по последовательности Фёльнера, позволяют доказать, что для любого непрерывного действия аменабельной группы на метрическом компакте найдётся инвариантная относительно этого действия мера.
Ссылки
- ↑ Боголюбов Н. Н., Крылов Н. М. (1937): «Общая теория меры в нелинейной механике». — Киев.
- ↑ N. N. Bogoliubov and N. M. Krylov (1937). «La theorie generalie de la mesure dans son application a l'etude de systemes dynamiques de la mecanique non-lineaire» (in French). Ann. Math. II 38: 65—113. Zbl. 16.86.
- ↑ «Николай Николаевич Боголюбов. Собрание научных трудов в 12 томах. РАН. Том 1: Математика». — М.: Наука, 2005. ISBN 5-02-034463-X.
Wikimedia Foundation. 2010.
Теорема Крылова — В теории динамических систем под теоремами Крылова Боголюбова понимаются две теоремы, утверждающие существование инвариантных мер у «хороших» отображений, определённых на «хороших» пространствах. Теоремы доказаны математиком… … Википедия
Теорема Боголюбова (значения) — Теорема Боголюбова «об острие клина» Теорема Боголюбова Парасюка Теорема Крылова Боголюбова … Википедия
КРЫЛОВА - БОГОЛЮБОВА МЕТОД УСРЕДНЕНИЯ — метод, применяемый в теории нелинейных колебаний для исследования колебательных процессов, основанный на принципе усреднения (осреднения), заменяющем точное дифференциальное уравнение движения усредненным. Различные схемы усреднения (Гаусса, Фату … Математическая энциклопедия
Боголюбов, Николай Николаевич — Николай Николаевич Боголюбов Дважды Герой Социалистического Труда Н. Н. Боголюбов Дата рождения: 8 (21) августа … Википедия
Боголюбов Н. Н. — Николай Николаевич Боголюбов Дата рождения: 21 августа 1909 Место рождения: Нижний Новгород Дата смерти: 13 февраля 1992 Место смерти: Москва Гражданство … Википедия
Боголюбов Николай Николаевич — Николай Николаевич Боголюбов Дата рождения: 21 августа 1909 Место рождения: Нижний Новгород Дата смерти: 13 февраля 1992 Место смерти: Москва Гражданство … Википедия
Николай Николаевич Боголюбов — Дата рождения: 21 августа 1909 Место рождения: Нижний Новгород Дата смерти: 13 февраля 1992 Место смерти: Москва Гражданство … Википедия
Крылов, Николай Митрофанович — В Википедии есть статьи о других людях с такой фамилией, см. Крылов. Николай Митрофанович Крылов Дата рождения: 17 (29) ноября 1879(1879 11 29) Место рождения: Петербург Дата смерти … Википедия
Крылов Николай Митрофанович — Николай Митрофанович Крылов Дата рождения: 16 (29) ноября 1879 Место рождения: Петербург Дата смерти: 11 мая 1955 Место смерти: Москва Гражданство: Россия Научная сфера: математика Альма матер … Википедия
Николай Митрофанович Крылов — Дата рождения: 16 (29) ноября 1879 Место рождения: Петербург Дата смерти: 11 мая 1955 Место смерти: Москва Гражданство: Россия Научная сфера: математика Альма матер … Википедия

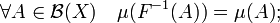
![\Pr [ X_{t} \in A | X_{0} = x ] = P_{t} (x, A).](http://dic.academic.ru/pictures/wiki/files/52/4d6443b4750a45ab883a031a57c57977.png)