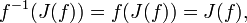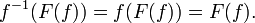Пыль фату

Множество Жюлиа

Множество Жюлиа

В голоморфной динамике, мно́жество Жюлиа́ 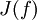$\, J(f)$ рационального отображения 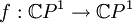$f:\C P^1\to \C P^1$ — множество точек, динамика в окрестности которых в определённом смысле неустойчива по отношению к малым возмущениям начального положения. В случае, если f — полином, рассматривают также заполненное множество Жюлиа — множество точек, не стремящихся к бесконечности. Обычное множество Жюлиа при этом является его границей.

Множество Фату 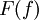$F(f)\,$ — дополнение к множеству Жюлиа. Иными словами, динамика итерирования f на 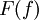$F(f)\,$ регулярна, а на 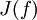$J(f)\,$ хаотична.

Эти множества названы по именам французских математиков Гастона Жюлиа и Пьера Фату, положивших начало исследованию голоморфной динамики в начале 20 века.

Определения

Пусть 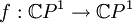$f:\C P^1\to \C P^1$ -- рациональное отображение. Множество Фату состоит из точек z, таких, что в ограничении на достаточно малую окрестность z последовательность итераций

$(f^n)_{n\in\mathbb{N}}$

образует нормальное семейство в смысле Монтеля. Множество Жюлиа -- дополнение к множеству Фату.

Это определение допускает следующую эквивалентную переформулировку: множество Фату это множество тех точек, орбиты которых устойчивы по Ляпунову. (Эквивалентность переформулировки неочевидна, но она следует из теоремы Монтеля.)

Свойства

• Как мгновенно следует из определений, множество Жюлиа всегда замкнуто, а множество Фату открыто.
• Множество Жюлиа для отображения степени, большей 1, всегда непусто (иначе можно было бы выбрать равномерно сходящуюся подпоследовательность из итераций.) В отношении же множества Фату аналогичное утверждение неверно: существуют примеры, в которых множество Жюлиа оказывается всей сферой Римана. 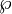Такой пример можно построить, взяв отображение $z\mapsto 2z (mod\, \Z [i])$ удвоения на торе $\C/\Z [i]$ (динамика которого, очевидно, везде хаотична), и пропустив его через $\wp$-функцию Вейерштрасса $\wp: \C/\Z [i] \to \C P^1$.
• Множество Жюлиа является замыканием объединения всех отталкивающих периодических орбит.
• Множества Фату и Жюлиа оба полностью инвариантны под действием f, то есть совпадают как со своим образом, так и с полным прообразом:

$\ f^{-1}(J(f)) = f(J(f)) = J(f),$

$\ f^{-1}(F(f)) = f(F(f)) = F(f).$

• Множество Жюлиа J(F) является границей (полного) бассейна притяжения любой притягивающей или суперпритягивающей орбиты; частным случаем этого является утверждение, что J(F) это граница заполненного множества Жюлиа (поскольку для полиномиального отображения бесконечность -- суперпритягивающая неподвижная точка, а заполненное множество Жюлиа есть дополнение к её бассейну притяжения). Кроме того, взяв полиномиальное отображение с тремя различными притягивающими неподвижными точками, получаем пример трёх открытых (естественно, несвязных) множеств на плоскости с общей границей.
• Если открытое множество U пересекает множество Жюлиа, то, начиная с некоторого достаточно большого n, образ 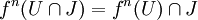$f^n(U\cap J) = f^n(U) \cap J$ совпадает со всем множеством Жюлиа J. Иными словами, итерации растягивают сколь угодно маленькую окрестность в множестве Жюлиа на всё множество Жюлиа.
• Поскольку указанное выше растяжение чаще всего происходит достаточно быстро, голоморфные отображения конформны, а множество Жюлиа инвариантно относительно динамики -- оно оказывается имеющим фрактальную структуру: его маленькие части похожи на большие.
• Если множество Жюлиа отлично от всей сферы Римана, то оно не имеет внутренних точек.
• Для всех точек z сферы Римана, кроме, быть может, двух, множество предельных точек последовательности полных прообразов f ^{− n}(z) есть множество Жюлиа. Это свойство применяется в компьютерных алгоритмах построения множества Жюлиа.

Связанные понятия

Квадратичное отображение 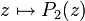$z\mapsto P_2(z)$ заменой координат всегда приводится к виду 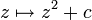$z\mapsto z^2 +c$. Оказывается, что множество Жюлиа будет связным, если и только если критическая точка z=0 (или, что то же самое, её образ z=c) не уходит на бесконечность. В случае, если итерации 0 стремятся к бесконечности, множество Жюлиа (совпадающее, в этом случае, с заполненным множеством Жюлиа) оказывается гомеоморфным канторову множеству, и имеет меру ноль. В этом случае его называют пылью Фату (несмотря на сбивающее с толку название, это именно множество Жюлиа -- множество хаотической динамики!).

Множество параметров c, при которых множество Жюлиа квадратичной динамики связно, называется множеством Мандельброта. Оно также имеет фрактальную структуру (и является, вероятно, одним из наиболее знаменитых фракталов).

Ссылки

• Дж. Милнор, Голоморфная динамика, Ижевск: РХД, 2000.
• Простая программа для генерирования множеств Жюлиа (Windows, 370 кБ)