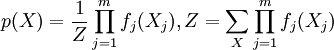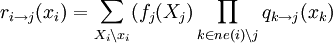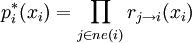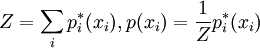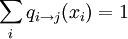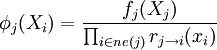Алгоритм sum-product

Алгоритм sum-product

Связать^?

Алгоритм «sum-product» — алгоритм маргинализации с помощью двунаправленной передачи сообщений на графе

Постановка задачи

Рассмотрим функцию:

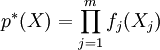$p^*(X) = \prod^m_{j=1}f_j(X_j)$, где $X_j = \{x_i\}_{i = 1}^n$

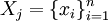
Чтобы получить вероятность, необходимо ее нормализовать:

$p(X) = \frac{1}{Z} \prod^m_{j=1}f_j(X_j), Z = \sum_X \prod^m_{j=1}f_j(X_j)$

Нас интересуют следующие задачи:

• 1. Задача нормализации

найти $Z = \sum_X \prod^m_{j=1}f_j(X_j)$

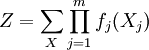
• 2. Задача маргинализации

найти $p^*_i(x_i) = \sum_{k \neq i}p^*(X)$

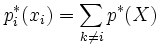
• 3. Задача нормализованной маргинализации

найти $p_i(x_i) = \sum_{k \neq i}p(X)$

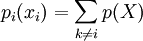
Все эти задачи являются NP-трудными, так что сложность их решения в худшем случае возрастает экспоненциально. Однако некоторые частные случаи можно решить быстрее, чем и занимается данный алгоритм.

Структура графа

Граф, используемый алгоритмом, состоит из вершин, соответствующих переменным, и вершин, соответствующих функциям. Функции соединены с переменными, от которых они зависят.

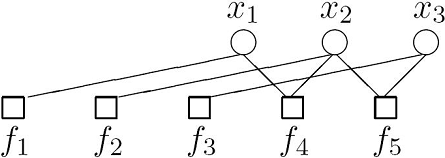
Пример

Например функции

p ^* (X) = f₁(x₁)f₂(x₂)f₃(x₃)f₄(x₁,x₂)f₅(x₂,x₃)

соответствует следующий граф:

Передача сообщений

В графе пересылаются сообщения двух видов: от функций к переменным и от переменных к функциям.

От переменной x_i к функции f_j:

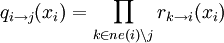$q_{i \to j}(x_i) = \prod_{k \in ne(i) \setminus j} r_{k \to i}(x_i)$ (здесь ne(i) — множество вершин, соседних с i)

От функции f_j к переменной x_i:

$r_{i \to j}(x_i) = \sum_{X_i \setminus x_i}(f_j(X_j) \prod_{k \in ne(i) \setminus j}q_{k \to j}(x_k)$

При этом пустое произведение считаем равным единице. Из этих формул видно, что если у вершины всего один сосед, то ее сообщение можно вычислить не зная входящих сообщений.

Алгоритм

Существует два подхода, в зависимости от характера полученного графа.

Подход 1

Предположим, что граф является деревом. Начиная с листьев будем постепенно обходить все вершины и вычислять сообщения (при этом применяется стандартное правило передачи сообщений: сообщение можно передавать только если его можно полностью построить).

Тогда за количество шагов, равное диаметру графа, работа алгоритма закончится.

Подход 2

Если граф не является деревом, то можно начать с того, что все переменные передают сообщение 1, а потом уже его модифицируют, когда до них доходят сообщения от функций.

Такой алгоритм в общем случае работает неверно и делает много лишнего, но все же полезен на практике.

Вычисление маргиналов

Когда рассылка сообщений закончена, маргиналы вычисляются по следующей формуле:

$p^*_i(x_i) = \prod_{j \in ne(i)}r_{j \to i}(x_i)$

$Z = \sum_i p^*_i(x_i), p(x_i) = \frac{1}{Z}p^*_i(x_i)$

Нормализация на лету

Если нужно рассчитать только нормализованные маргиналы (настоящие вероятности), то можно на каждом шаге нормализовать сообщения от переменных к функциям:

$q_{i \to j}(x_i) = \alpha_{ij} \prod_{k \in ne(i) \setminus j} r_{k \to i}(x_i)$,

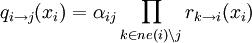где α_ij подобраны так, чтобы

$\sum_i q_{i \to j}(x_i) = 1$

Математическое обоснование алгоритма

С математической точки зрения алгоритм изначальное разложение

$p^*(X) = \prod^m_{j=1}f_j(X_j)$

перераскладывает в произведение

$p^*(X) = \prod^m_{j=1}\phi_j(X_j) \prod^m_{i=1}\psi_i(x_i)$,

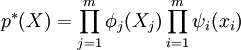где φ_j соответствует узлам-функциям, а ψ_i — узлам-переменным.

Изначально, до передачи сообщений φ_j(X_j) = f_j(X_j) и ψ_i(x_i) = 1

Каждый раз, когда приходит сообщение 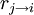$r_{j \to i}$ из функции в переменную, φ и ψ пересчитываются:

$\psi_i(x_i) = \prod_{j \in ne(i)}r_{j \to i}(x_i)$,

$\phi_j(X_i) = \frac{f_j(X_j)}{\prod_{i \in ne(j)}r_{j \to i}(x_i)}$

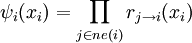Очевидно, что общее произведение от этого не меняется, а ψ_i по окончании передачи сообщений станет маргиналом p ^* (x_i).

Ссылки

С. Николенко. Курс «Вероятностное обучение»