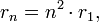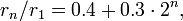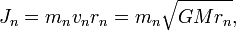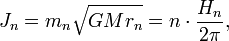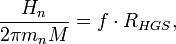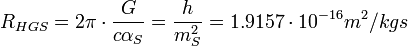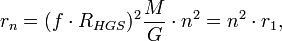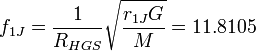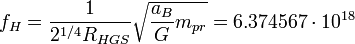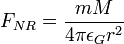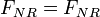- Солнечная система как гравитационный атом Бора
-
Солнечная система как гравитационный атом Бора
Солнечная система как гравитационный атом Бора - представление Солнечной планетной системы в виде модели "гравитационного атома Бора" с радиусом произвольной орбиты в общем виде:
где
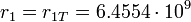 м - радиус первой орбиты (не обязательно заполненной) планет земной группы (n = 3,4,5,6,8), и
м - радиус первой орбиты (не обязательно заполненной) планет земной группы (n = 3,4,5,6,8), и 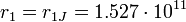 м - радиус первой орбиты (заполнен обязательно, правда планетой другого типа) внешних планет (n = 2,3,4,5,6).
м - радиус первой орбиты (заполнен обязательно, правда планетой другого типа) внешних планет (n = 2,3,4,5,6).Содержание
История
В астрономии известно правило Тициуса — Боде, которое представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Правило было предложено И. Д. Тициусом в 1766 г. и получило известность благодаря работам И. Э. Боде в 1772 г. [1]:
где
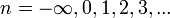 , а расстояния измеряются в астрономических единицах. Долгое время эта математическая формула не имела физического обоснования, но с появлением квантовой физики денлались неоднократные попытки ее объяснения [2] [3] [4] [5]. Дело в том, что при рассмотрении атома Бора на начальном этапе делались попытки перенесения теории планетной системы на электронные орбиты атома. Но с появлением уравнения Шредингера и развития квантовой механики начался обратный процесс — перенесения квантовомеханических представлений на строение Солнечной системы.
, а расстояния измеряются в астрономических единицах. Долгое время эта математическая формула не имела физического обоснования, но с появлением квантовой физики денлались неоднократные попытки ее объяснения [2] [3] [4] [5]. Дело в том, что при рассмотрении атома Бора на начальном этапе делались попытки перенесения теории планетной системы на электронные орбиты атома. Но с появлением уравнения Шредингера и развития квантовой механики начался обратный процесс — перенесения квантовомеханических представлений на строение Солнечной системы.Успех пришел только в конце 90-х годов 20-го века и связан с исследованием югославского физика Рубчича [6] [7] [8] [9] А также бразильской группой космологов под руководством Карнейро [10] [11] [12] и других [13].
Наиболее полно даный процесс представлен в сборнике статей [9]. В это же время был разработан т. н. «диффузный подход» к уравнению Шредингера для рассмотрения процесса создания Солнечной системы. Очевидно, что при таком подходе решения и масштабные константы «макроскопического уравнения Шредингера» получаются численным путем, что затрудняет рассмотрение данного вопроса.
Модель гравитационного квантования орбит
В общем случае момент импульса для произвольной планеты можно представить в виде:
где G - гравитационная постоянная, mn - масса планеты, M - масса звезды (
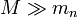 ), а rn - радиус орбиты планеты.
), а rn - радиус орбиты планеты.Предположим, что в этом случае макроскопической квантовой системы также можно воспользоватиься микроскопическим квантованием момента импульса (типа Бора- Зоммерфельда):
где Hn - «макроскопический» квант действия для произвольной планеты (он зависит от n- номера орбиты). Этот квант действия можно записать в виде:
где
Унивесиальная постоянная, имеющая размерность гравитационного сопротивления (гравитационная постоянная фон Клитцинга), а mS - масса масштаба Стони, f- гравитационный фактор коррекции, учитывающий макроскопические размеры квантовой системы.
В общем случае радиус орбиты произвольной планеты можно представить в виде:
где
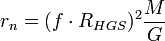 - радиус орбиты первой планеты (n = 1). Зная параметры орбит планетной системы, можно определить гравитационный фактор коррекции:
- радиус орбиты первой планеты (n = 1). Зная параметры орбит планетной системы, можно определить гравитационный фактор коррекции: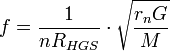 .
.
Очевидно, что он зависит от массы центрального тела (M) и поэтому не может выступать в качестве фундаментальной постоянной. Совсем другое дело – радиус первой орбиты r1, который должен быть фундаментальной константой по аналогии с обычным атомом Бора, где существует фундаментальный радиус Бора (масштаб):
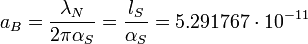 м
м
Где λN- комптоновская длина волны электрона, а
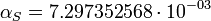 - силовая постоянная масштаба Стони (постоянная тонкой структуры Зоммерфельда).
- силовая постоянная масштаба Стони (постоянная тонкой структуры Зоммерфельда).Использование «диффузионного» уравнения Шредингера для планетной системы не предсказывает конкретное значение для «гравитационного радиуса Бора». Поэтому можно использовать непосредственно уравнение Шредингера для движения частицы с массой Планка (mP), например в гравитационном поле другой планковской частицы. В этом случае мы получаем фундаментальное значение для гравитационного радиуса Бора в виде:
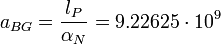 м
м
где
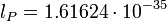 - длина Планка, а
- длина Планка, а 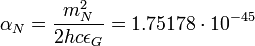 - силовая постоянная природного масштаба, mN- масса электрона, h- постоянная Планка, c- скорость света и
- силовая постоянная природного масштаба, mN- масса электрона, h- постоянная Планка, c- скорость света и 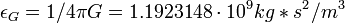 - диэлектрическая гравитационная постоянная.
- диэлектрическая гравитационная постоянная.Не трудно заметить, что первый радиус гравитационной орбиты для планет земной группы близок к значению:
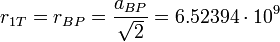 м
м
Т.е. определяется масштабом Планка! Гравитационный фактор коррекции в этом случае будет:
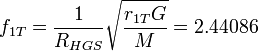 .
.
При использовании уравнения Шредингера для движения частицы с массой Стони (mS) в гравитационном поле другой частицы Стони, мы получаем следующее значение для гравитационного радиуса Бора масштаба Стони:
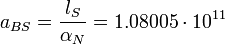 м
м
где
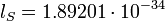 м – длина масштаба Стони. Но именно это значение радиуса орбиты имеет сегодня планета Венера! Далее, первый радиус орбиты внешних планет Солнечной системы равен значению:
м – длина масштаба Стони. Но именно это значение радиуса орбиты имеет сегодня планета Венера! Далее, первый радиус орбиты внешних планет Солнечной системы равен значению: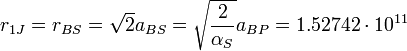 м,
м,
Которое практически совпадает с современным значением для орбиты Земли! Таким образом, внешние планеты Солнечной системы определяются масштабом Стони. Гравитационный фактор коррекции в этому случае будет:
Для сравнения можно привести значение фактора коррекции для атома Бора:
где mpr- масса протона, а также для «планкионного атома»:
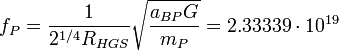 .
.
Очевидно, что эти «микроскопические» значения очень сильно отличаются от «макроскопических». Другими словами, мы имеем значительное «ослабление» гравитационного фактора при переходе к макроскопическим квантовым системам.
Таблица 1. Внутренние планеты земного типа.
Название тела Радиус тела, м Радиус орбиты, м Масса тела, кг 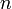
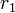 м
м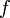
Меркурий 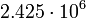
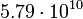
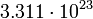
3 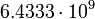
2.42386 Венера 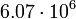
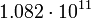
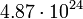
4 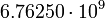
2.48509 Земля 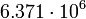
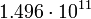
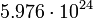
5 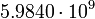
2.33768 Марс 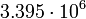
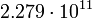
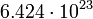
6 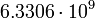
2.40442 Планетарные параметры были взяты в справочнике Алена (1973) [14].
Таблица 2. Внешние планеты.
Название тела Радиус тела, м Радиус орбиты, м Масса тела, кг 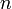
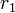 м
м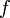
Юпитер 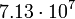
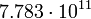
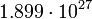
2 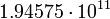
13.33301 Сатурн 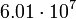
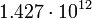
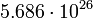
3 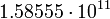
12.03317 Уран 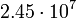
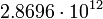
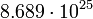
4 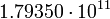
12.7979 Нептун 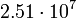
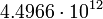
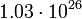
5 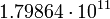
12.8163 Плутон 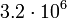
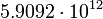
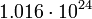
6 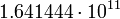
12.24341 Квантовое гравитационное уравнение Шредингера
При описании планетной системы сегодня используется следующая форма записи уравнения Шредингера:
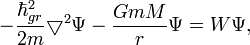 ,
,
где m- масса планеты, а M- масса центральной звезды. При этом в жертву была принесена т.н. «гравитационная постоянная Планка, которая здесь перестала быть фундаментальной величиной:
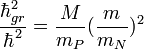 ,
,
где mP- масса Планка, а mN- масса электрона. Дело в том, что в этом случае гравитационная постоянная Планка имеет различные значения для разных планет и звезд.
Более перспективном является следующая форма записи гравитационного уравнения Шредингера:
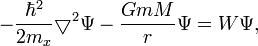 ,
,
в которой используется концепция «малой виртуальной массы»:
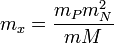 .
.
Следует отметить, что оба подхода дают одинаковые результаты для масштабных значений гравитационного атома Бора. Действительно, гравитационный радиус Бора имеет значение:
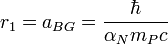 ,
,
а гравитационная энергия связи Бора:
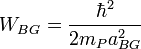 ,
,
где
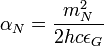 - силовая постоянная гравитационного взаимодействия, а
- силовая постоянная гравитационного взаимодействия, а 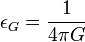 - гравитационная «диэлектрическая постоянная».
- гравитационная «диэлектрическая постоянная».Результаты расчета гравитационной постоянной Планка и «малой виртуальной массы» представлены в Таблицах 3,4:
Таблица 3. Внутренние планеты земного типа.
Название тела Радиус тела, м Радиус орбиты, м Масса тела, кг 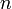
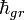 Дж с
Дж с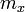 кг
кгМеркурий 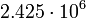
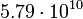
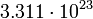
3 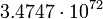
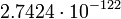
Венера 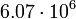
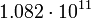
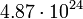
4 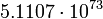
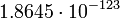
Земля 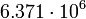
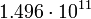
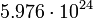
5 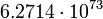
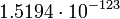
Марс 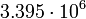
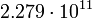
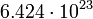
6 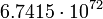
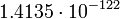
Таблица 4. Внешние планеты.
Название тела Радиус тела, м Радиус орбиты, м Масса тела, кг 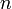
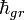 Дж с
Дж с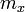 кг
кгЮпитер 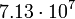
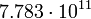
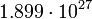
2 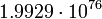
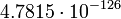
Сатурн 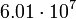
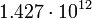
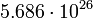
3 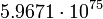
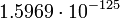
Уран 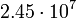
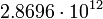
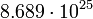
4 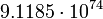
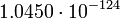
Нептун 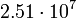
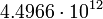
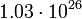
5 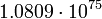
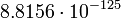
Плутон 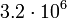
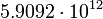
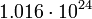
6 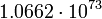
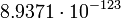
Виртуальная масса центрального тела
Сверхмалое значение виртуальной массы планеты должно компенсироваться большим значением «виртуальной массы» центрального тела Mx. Это значение может быть найдено следующим образом. Рассмотрим силу Ньютона для реальных масс:
А также силу Ньютона для виртуальных масс в виде:
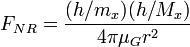 .
.
Далее используя равенство этих сил:
можно найти виртуальную массу центрального тела:
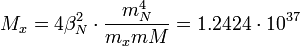 кг,
кг,
в случае Солнечной системы, где
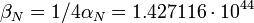 . Таким образом, отсутствие корректного введения «гравитационных монополей» приводит к спекуляциям различного рода, как в области паранауки (различные «торсионные поля»), так в области подлинной науки (введение т.н. «темной материи») и т.д.
. Таким образом, отсутствие корректного введения «гравитационных монополей» приводит к спекуляциям различного рода, как в области паранауки (различные «торсионные поля»), так в области подлинной науки (введение т.н. «темной материи») и т.д.Смотри также
Ссылки
- ↑ Symposium on the origin of the Solar System. (1972) Raris, Edition du Centre National de la Recherche Scientifique.
- ↑ Caldirola P, Pavisic M and Recami E, Nuov.Cim. 48B (1978) 205.
- ↑ Sivaram C and Sinha KP, Phys.Reports 51 (1979) 111.
- ↑ L. Nottale, G. Schumacher and J. Gay, A&A, 332 (1997) 1018.
- ↑ Godel K, Rev.Mod.Phys. 21 (1949) 447.
- ↑ A. Rubcic and J. Rubcic, Fizika B 4 (1995) 11
- ↑ A. Rubcic and J. Rubcic, Fizika B 7 (1998) 1
- ↑ A. Rubcic and J. Rubcic, Fizika B 5 (1996) 85
- ↑ 1 2 ANTUN RUBCIC and JASNA RUBCIC. SQUARE LAW FOR ORBITS IN EXTRA-SOLAR PLANETARY SYSTEMS.Quantization in Astrophysics, Brownian Motion, and Supersymmetry. Editors: F.Smarandache and V.Christanto. MathTiger, 2007, Chennai, Tamil Nadu, India. ISBN 819021909X.
- ↑ Saulo Carneiro (1997). The Large Numbers Hypothesis and Quantum Mechanics. arxiv:gr-qc/9712014v1
- ↑ M. Oliveira Neto and L.A. Maia, Advances in Space Dynamics, A. F. Bertachini, Editor, pp 456—470 (2000).
- ↑ Marcal de Oliveira Neto, Liliane de Almeida Maia, Saulo Carneiro. A DESCRIPTION OF EXTRA-SOLAR PLANETARY ORBITS THROUGH A SCHRODINGER — TYPE DIFFUSION EQUATION. ADVANCES IN SPACE DYNAMICS 4: CELESTIAL MECHANICS AND ASTRONAUTICS, H. K. Kuga, Editor, 113—121 (2004).
- ↑ A. G. Agnese and R. Festa, Phys. Lett. A, 227 (1997) 165.
- ↑ Allen C.W.(1973). Astrophysical quantities. 3-d edition. University of London, The Athlone Press.
Литература
- Д.тер Хаар. Некоторые замечания о теориях происхождения Солнечной системы из первичной солнечной туманности. с.107.
- С.Ф.Дермонт. Закон Боде и преобладание приблизительной соизмеримости среди пар орбитальных периодов в Солнечной системе. с. 466.
- Происхождение солнечной системы Под реакцией Г.Ривса.М.:Мир,1976. 570с.
Wikimedia Foundation. 2010.