Полукольцо (теория множеств)

Полукольцо (теория множеств)

Полукольцо (в теории множеств) — система множеств S, для которой выполнены следующие условия:

• $\varnothing \in S$;
• $\forall A, B \in S \quad A\cap B \in S$;
• $\forall A \in S, A_1 \in S \quad A_1 \subset A \Rightarrow \exists A_2, \dots, A_n \subset A : A_1 \sqcup \dots \sqcup A_n = A$.

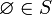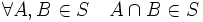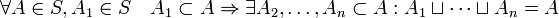Таким образом, полукольцо содержит в себе пустое множество, замкнуто относительно пересечения и любое множество из полукольца представимо в виде конечного объединения дизъюнктных (попарно не пересекающихся) множеств, принадлежащих этому полукольцу. Полукольцо не замкнуто относительно объединения множеств.

Полукольцом с единицей называют полукольцо с таким элементом E, что его пересечение с любым элементом A полукольца равно A. Применяя метод математической индукции, можно расширить последний пункт определения: если множества 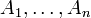$A_1, \dots, A_n$ являются элементами полукольца и подмножествами элемента A, то их можно дополнить непересекающимися элементами 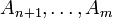$A_{n+1}, \dots, A_m$ до A. Любое кольцо является полукольцом. Прямое произведение полуколец также является полукольцом.

Примеры полуколец

  1.	<N,+,•>, где N – множество неотрицательных целых чисел с обычными операциями + и •;
  2.	<{0},+,•> - тривиальное полукольцо;
  3.	Двухэлементные полукольца:<Z2 ,+,•>, <В,+,•> (в В 1+1=1);
  4.	Множество матриц  с элементами из полукольца N и операциями + и  ;
  5.	Множества N, Z, Q+, Q, R+, R и введенных на них различных комбинаций операций: обычные сложение и умножение, максимум   и минимум   двух чисел, НОД и НОК, когда они определены.

Свойства полуколец

 Непустое множество S с бинарными операциями + и • называется полукольцом, если выполняются следующие аксиомы:
  1.	(S,+) – коммутативная полугруппа с нейтральным элементом 0;
    •	Ассоциативность: </math>(\forall a,b \in S)(a+b)+c=a+(b+c)</math> ;
    •	Коммутативность: </math>(\forall a,b \in S)(a+b)=(b+a)</math> ;
    •	Существование нейтрального элемента: (\exists 0 \in S)(\forall a \in S)(0+a=a+0=a) .
  2.	(S,•) – полугруппа:
    •	Ассоциативность: </math>(\forall a,b \in S)(a*b)*c=a*(b*c)</math> ;
  3.	Умножение дистрибутивно относительно сложения:
    •	левая дистрибутивность: </math>(\forall a,b \in S) а*(в+с)=ав+ас</math> ;
    •	правая  дистрибутивность: </math>(\forall a,b \in S) (а+в)*с=а*с+в*с</math> .
  4.	Мультипликативное свойство 0:
    •	</math>(\forall a \in S) (a*0=0*a=0)</math> .
 Эта аксиоматика появилась в 1934 году и ее автором является Вандовер.
 Полукольцо S называется коммутативным, если операция в нем коммутативна: </math>(\forall a,b \in S) (a*b=b*a)</math> .
 Полукольцо S называется полукольцом с единицей, если в нем существует нейтральный элемент по умножению, который называется единицей: </math>(\exists 1 \in S)(\forall a \in S)(1*a=a*1=a)</math> 
 Полукольцо с импликацией </math>a*c=b*c (a+c=b+c) \Rightarrow a=b</math> называется мультипликативно (аддитивно) сократимым.
 Полукольцо, в котором выполняется равенство a*a=a (a+a=a)   , называется мультипликативно (аддитивно) идемпотентным.

Примечания

См. также

• Алгебра

Ссылки