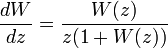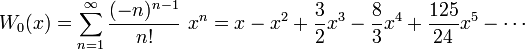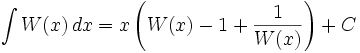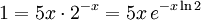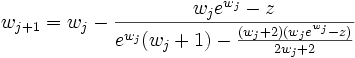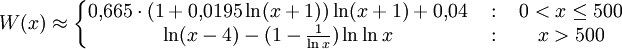Функция Ламберта

W-функция Ламберта определяется как обратная функция к f(w) = we^w, для комплексных w. Обозначается W(x) или 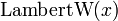$\operatorname{LambertW}(x)$. Для любого комплексного z она определяется функциональным уравнением:

z = W(z)e^W(z)

W-функция Ламберта не может быть выражена в элементарных функциях. Она применяется в комбинаторике, например, при подсчёте числа деревьев, а также при решении уравнений.

История

Функция изучалась ещё в работе Леонарда Эйлера в 1779, но не имела самостоятельного значения и названия вплоть до 1980-х. Как самостоятельная функция была введена в системе компьютерной алгебры LambertW. Имя Иоганна Генриха Ламберта было выбрано, поскольку Эйлер ссылался в своей работе на труды Ламберта, и поскольку «называть ещё одну функцию именем Эйлера было бы бесполезно»^[1]

Многозначность

График W₀(x) для −1/e ≤ x ≤ 4

Поскольку функция f(w) не является инъективной на интервале 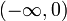$(-\infty,0)$, W(z) является многозначной функцией на [ − 1 / e,0). Если ограничиться вещественными 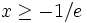$x\ge-1/e$ и потребовать 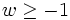$w\ge -1$, будет определена однозначная функция W₀(x).

Свойства

С помощью дифференцирования неявной функции можно получить, что при 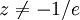$z\ne -1/e$ функция Ламберта удовлетворяет следующему дифференциальному уравнению

${dW\over dz} = \frac{W(z)}{z(1+W(z))}$

С помощью теоремы об обращении рядов можно получить выражение для ряда Тейлора; он в окрестности нуля сходится при | z | < 1 / e:

$W_0(x)=\sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac{3}{2}x^3 - \frac{8}{3}x^4 + \frac{125}{24}x^5 - \cdots$

С помощью интегрирования по частям можно найти интеграл от W(z):

$\int W(x)\, dx = x \left( W(x) - 1 + \frac{1}{W(x)} \right) + C$

Значение в некоторых точках

$W\left(-\frac{\pi}{2}\right) = \frac{i\pi}{2}$

$W\left(-{1\over e}\right) = -1$

$W\left(-\frac{\ln 2}{2}\right)= -\ln 2$

$W(0) = 0\,$

$W(e) = 1\,$

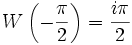
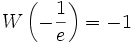
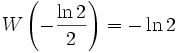
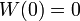
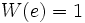
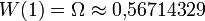$W(1) = \Omega \approx 0{,}56714329\,$ (постоянная Омега)

Решение уравнений с помощью W-функции

Решения многих трансцендентных уравнений могут быть выражены в форме W-функции.

Пример: x^x = z

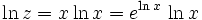$\ln z=x\ln x=e^{\ln x}\,\ln x$, следовательно, x = e^W(lnz).

Пример: 2^x = 5x

$1 = 5 x\cdot 2^{-x} = 5 x\, e^{-x\ln 2}$

Обозначим y = − xln2, тогда 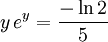$y\,e^y={-\ln 2\over 5}$, отсюда 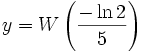$y=W\left({-\ln 2\over 5}\right)$ и окончательно $x=-{1\over\ln2}W\left({-\ln 2\over 5}\right)$.

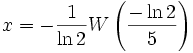Вычисление

W-функция может быть приблизительно вычислена с помощью рекуррентного соотношения^[1]:

$w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)} {2w_j+2}}$

Пример программы на языке Python:

import math
class Error(Exception):
    pass
def lambertW(x, prec=1e-12):
    w = 0
    for i in xrange(100):
        wTimesExpW = w*math.exp(w)
        wPlusOneTimesExpW = (w+1)*math.exp(w)
        if prec>abs((x-wTimesExpW)/wPlusOneTimesExpW):
            break
            w = w-(wTimesExpW-x)/(wPlusOneTimesExpW-(w+2)*(wTimesExpW-x)/(2*w+2))
 	else:
            raise Error, "W(x) не сходится достаточно быстро при x=%f"%x
        return w

Для приближённого вычисления можно использовать формулу^[2]:

$W(x) \approx \left\{ \begin{matrix} 0{,}665\cdot (1+0{,}0195\ln(x+1))\ln(x+1) + 0{,}04 &amp;amp; \ :\ &amp;amp; 0&amp;lt;x\le500 \\ \ln(x-4) - (1-{1\over\ln x}) \ln\ln x &amp;amp; \ :\ &amp;amp; x&amp;gt;500 \\ \end{matrix} \right.$

Ссылки

1. ↑ ^{1 2} Corless et al. "On the Lambert W function" Adv. Computational Maths. 5, 329 - 359 (1996) (↑ Double precision function LAMBERTW(X) в пакете QCDINS