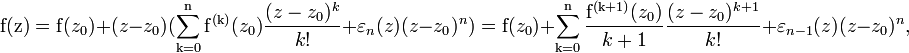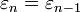Формула Тейлора — Пеано — Форmула Тейлора Пеано Пусть , z0 предельная точка множества Df и . Если функция f n дифференцируема в смысле Ферма Лагранжа в точке z0, то справедлива формула Тейлора Пеано … Википедия
Формула Тейлора — Пеано Пусть , предельная точка множества и . Если функция дифференцируема в смысле Ферма Лагранжа в точке , то справедлива формула Тейлора Пеано … Википедия
Пеано — Пеано, Джузеппе Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более… … Википедия
Пеано Д. — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен… … Википедия
Пеано Джузеппе — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен… … Википедия
Пеано, Джузеппе — Джузеппе Пеано Джузеппе Пеано (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию мат … Википедия
Джузеппе Пеано — (Giuseppe Peano; 1858 1932) итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино сине флексионе. Более всего известен как автор стандартной… … Википедия
ТЕЙЛОРА ФОРМУЛА — представление функции в виде суммы еи многочлена Тейлора степени п(n=0, 1, 2, . . .) и остаточного члена. Если действительная функция / одного переменного имеет ппроизводных в точке х 0, то ее Т. ф. имеет вид f(x) = Pn(x) + rn(x), где Тейлора… … Математическая энциклопедия
Ряд Тейлора — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а… … Википедия
Многочлен Тейлора — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды… … Википедия
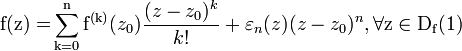
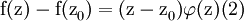
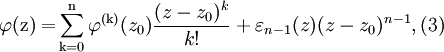
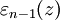 - непрерывная в точке z0 функция и
- непрерывная в точке z0 функция и 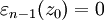 . Из равенств (2) и (3) получаем:
. Из равенств (2) и (3) получаем: