Распределение Гаусса

Нормальное распределение

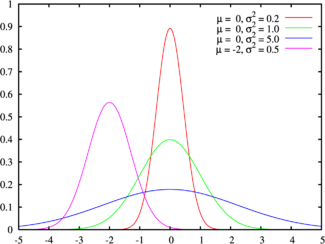
Плотность вероятности Красная линия соответствует стандартному нормальному распределению
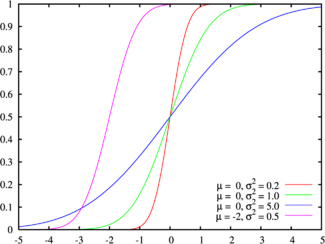
Функция распределения Цвета на этом графике соответствуют графику наверху
Параметры	μ - коэффициент сдвига (вещественное число) σ > 0 - коэффициент масштаба (вещественный, строго положительный)
Носитель	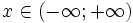$x \in (-\infty;+\infty)\!$
Плотность вероятности	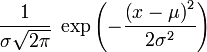$\frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!$
Функция распределения	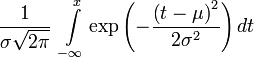$\frac1{\sigma\sqrt{2\pi}}\;\int\limits_{-\infin}^{x} \exp\left(-\frac{\left(t-\mu\right)^2}{2\sigma^2} \right) dt\!$
Математическое ожидание	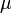$\mu\,$
Медиана	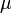$\mu\,$
Мода	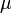$\mu\,$
Дисперсия	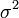$\sigma^2\,$
Коэффициент асимметрии	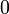$0\,$
Коэффициент эксцесса	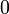$0\,$
Информационная энтропия	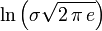$\ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!$
Производящая функция моментов	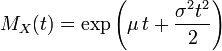$M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right)$
Характеристическая функция	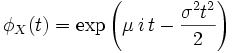$\phi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)$

Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Статистическая проверка принадлежности нормальному распределению

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии проверки на «нормальность»:

• Критерий Пирсона
• Критерий Колмогорова-Смирнова
• Критерий Андерсона-Дарлинга(англ.)
• Критерий Жака-Бера(англ.)
• Критерий Шапиро-Вилка(англ.)
• «График нормальности»(англ.) — не столько критерий, сколько графическая иллюстрация: точки специально построенного графика должны лежать почти на одной прямой.

Заключение

Нормальное распределение наиболее часто встречается в природе, нормально распределёнными являются следующие случайные величины:

• отклонение при стрельбе
• ошибки при измерениях
• рост человека

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Доказано, что сумма очень большого числа случайных величин, влияние каждой из которых близко к 0, имеет распределение, близкое к нормальному. Этот факт является содержанием предельной теоремы Ляпунова.

См. также

• Аддитивный белый гауссовский шум
• Логнормальное распределение
• Центральная предельная теорема
• Двумерное нормальное распределение

Вероятностные распределения Одномерные Многомерные Дискретные: Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | равномерное мультиномиальное Абсолютно непрерывные: Бета | Вейбулла | Гамма | Колмогорова | Коши | Лапласа | логнормальное | Лоренца | нормальное (Гаусса) | равномерное | Парето | Стьюдента | Фишера | хи-квадрат | экспоненциальное | Эрланга многомерное нормальное

править