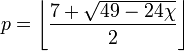Раскраска графов

Проблема четырёх красок

Проблема четырёх красок — математическая задача, предложенная Гутри (англ.) в 1852 году.

Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.

Иначе говоря, показать что хроматическое число плоского графа не превосходит 4.

Эквивалентные формулировки

Рёбра произвольной триангуляции сферы можно раскрасить в три краски так, чтобы все стороны каждого треугольника были раскрашены в разные цвета.

О доказательстве

К. Аппель и В. Хакен доказали в 1976 г., что так можно раскрасить любую карту. Это была первая крупная математическая теорема, для доказательства которой был применён компьютер. Несмотря на последующие упрощения, доказательство практически невозможно проверить, не используя компьютер. Поэтому некоторые математики отнеслись к этому доказательству с недоверием, что объяснялось не только использованием компьютера, но и громоздкостью описания алгоритма первых доказательств (741 страница), впоследствии были предложены более компактные алгоритмы и скорректирован ряд ошибок^[1]. Проблема четырех красок является одним из известнейших прецедентов неклассического доказательства в современной математике.

Предыстория доказательства

Наиболее известные попытки доказательства:

• Альфред Кэмпе предложил доказательство в 1879^[2], его опровергли только в 1880, на основе его идей удалось доказать что любую карту можно раскрасить в 5 цветов.
• Питер Тайт предложил другое доказательство в 1880^[3], его опровергли в 1891.
• В своей книге^[4] Горбатов утверждает, что предложил классическое доказательство ещё в 1964, позже был предложен более короткий вариант доказательства ^[5], однако эти доказательства так и не получили всеобщего признания.

Вариации и обобщения

Аналогичные задачи для других поверхностей (тор, бутылка Клейна и т. д.) оказались значительно проще. Для всех замкнутых поверхностей кроме сферы и бутылки Клейна необходимое число красок может быть вычислено через эйлерову характеристику χ по формуле

$p=\left\lfloor\frac{7 + \sqrt{49 - 24 \chi}}{2}\right\rfloor$

Для бутылки Клейна число равно 6, а для сферы естественно 4.

В старших размерностях разумного обобщения задачи не существует.

Литература

1. ↑ R.Diestel Graph Theory, Electronic Edition — NY: Springer-Verlag, 2005, P. 137.
2. ↑ A. B. Kempe, On the geographical problem of the four colors, Amer. J. Math., 2 (1879), 193—200.
3. ↑ P. G. Tait, Note on a theorem in geometry of position, Trans. Roy. Soc. Edinburgh 29 (1880), 657—660.
4. ↑ В.А. Горбатов Фундаментальные основы дискретной математики. Информационная математика. — М.: Наука. Физматлит, 2000. — С. 253-254. — 544 с. — 2000 экз. — ISBN 5-02-015238-2
5. ↑ Чечулин В. Л. Об одном варианте доказательства 4-раскрашиваемости плоских графов // Вестник ПГУ, серия Математика. Механика. Информатика, г. Пермь — № 4(4), 2006 г., сс. 86-87.

• А. А. Зыков Основы теории графов. — М.: Вузовская книга, 2000. — С. 367—386. — 2004 экз.
• Р.Курант, Г.Роббинс Что такое математика?
• Самохин А. В. Проблема четырех красок: неоконченная история доказательства // СОЖ, 2000, No 7, с. 91—96.. Проверено 17 августа 2008.
• Родионов В. В. Методы четырехцветной раскраски вершин плоских графов. — М.: КомКнига, 2000. — 48 с. — 2005 экз. — ISBN 5-484-00127-7
• Thomas, Robin The Four Color Theorem