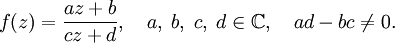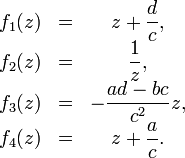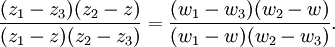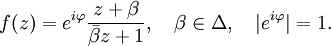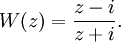Преобразование Мебиуса

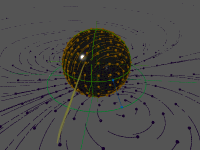Вид преобразований на комплексной плоскости (серая) и сфере Римана (чёрная)

Определение

Преобразование Мёбиуса — комплексная рациональная функция вида

$f(z)=\frac{az+b}{cz+d},\quad a,\;b,\;c,\;d\in\mathbb C,\quad ad-bc\ne 0.$

Частный случай дробно-линейных функций.

Легко проверяются следующие простые свойства:

1. Тождественное отображение f(z) = z также является частным случаем дробно-линейной функции. Достаточно подставить $a=d=1,\;b=c=0$.
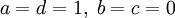2. Суперпозиция дробно-линейных отображений также будет представлять собой дробно-линейную функцию.
3. Функция, обратная дробно-линейной, также будет являться такой.

Отсюда следует, что дробно-линейные отображения будут образовывать группу относительно операции суперпозиции (группа автоморфизмов сферы Римана, именуемая также группой Мёбиуса). Эта группа является комплексно-трёхмерной группой Ли.

Алгебраические свойства

При умножении параметров a, b, c, d на ненулевое комплексное число преобразование не меняется. Говоря формально, группа Мёбиуса является проективизацией группы 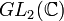$GL_2(\mathbb C)$, то есть имеет место эпиморфизм: $\left(\begin{matrix}a&&b\\c&&d\end{matrix}\right)\to\frac{az+b}{cz+d}$.

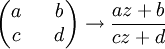Группа Мёбиуса изоморфна специальной ортохронной группе Лоренца $SO^\uparrow(1,\;3)$.

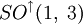Предположим, что матрица, соответствующая преобразованию, нормализована, то есть удовлетворяет условию ad − bc = 1. Тогда, в зависимости следа этой матрицы, равного a + d, можно классифицировать все дробно-линейные отображения на три типа:

• эллиптические — − 2 < a + d < 2;
• параболические — $a+d=\pm 2$;
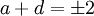• гиперболические — | a + d | > 2.

Геометрические свойства

Во-первых, очень важным фактом является то, что любое дробно-линейное отображение может быть представлено в виде комбинации сдвигов, инверсий, поворотов и растяжений. Это доказывается очень просто — произвольное отображение 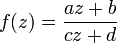$f(z)=\frac{az+b}{cz+d}$ разложимо в суперпозицию четырёх функций:

f(z) = f₄(f₃(f₂(f₁(z)))),

где

$\begin{matrix}f_1(z)&amp;amp;amp;=&amp;amp;amp;z+\dfrac{d}{c},\\f_2(z)&amp;amp;amp;=&amp;amp;amp;\dfrac{1}{z},\\f_3(z)&amp;amp;amp;=&amp;amp;amp;-\dfrac{ad-bc}{c^2}z,\\f_4(z)&amp;amp;amp;=&amp;amp;amp;z+\dfrac{a}{c}.\end{matrix}$

Во-вторых, непосредственно из этого сразу следует свойство сохранения углов и сохранения окружностей при дробно-линейном отображении, так как все отображения, входящие в суперпозицию, конформны. Обратим внимание, что подразумеваются окружности на сфере Римана, в число которых входят прямые на плоскости.

Далее, для произвольных трёх точек 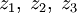$z_1,\;z_2,\;z_3$ существует единственное дробно-линейное отображение, переводящее эти три точки в фиксированные три точки 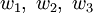$w_1,\;w_2,\;w_3$. Это отображение строится простейшим образом, исходя из того, что дробно-линейные отображения сохраняют ангармоническое отношение четырёх точек комплексной плоскости. Искомое отображение будет строиться заменой одной из точек и её образа на переменную, соответственно, z и w; оно будет иметь общий вид:

$\frac{(z_1-z_3)(z_2-z)}{(z_1-z)(z_2-z_3)}=\frac{(w_1-w_3)(w_2-w)}{(w_1-w)(w_2-w_3)}.$

Преобразование Мёбиуса и единичный круг

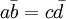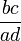Преобразование Мёбиуса (az + b) / (cz + d) является автоморфизмом единичного круга Δ = {z: | z | < 1} тогда и только тогда, когда $a{\bar b}=c{\bar d}$ и $\frac{bc}{ad}$ принадлежит полуинтервалу $[0,\;1)$.

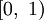Как для сферы Римана, так и для единичного круга дробно-линейными функциями исчерпываются все конформные автоморфизмы. Автоморфизмы единичного круга образуют вещественно-трёхмерную подгруппу группы Мёбиуса; каждый из них выражается в виде:

$f(z)=e^{i\varphi}\frac{z+\beta}{{\bar\beta}z+1},\quad\beta\in\Delta,\quad|e^{i\varphi}|=1.$

Примеры

Одним из важных примеров дробно-линейной функции является преобразование Кэли:

$W(z)=\frac{z-i}{z+i}.$

Оно связывает две канонические области на комплексной плоскости, отображая верхнюю полуплоскость 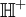${\mathbb H}^+$ в единичный круг Δ.

Далее, для произвольных трех точек 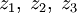$z_1,\;z_2,\;z_3$ существует единственное дробно-линейное отображение, переводящее эти три точки в фиксированные три точки 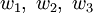$w_1,\;w_2,\;w_3$. Это отображение строится простейшим образом, исходя из того, что дробно-линейные отображения сохраняют ангармоническое отношение четырёх точек комплексной плоскости. Искомое отображение будет строиться заменой одной из точек и её образа на переменную, соответственно, z и w; оно будет иметь общий вид:

$\frac{(z_1-z_3)(z_2-z)}{(z_1-z)(z_2-z_3)}=\frac{(w_1-w_3)(w_2-w)}{(w_1-w)(w_2-w_3)}.$

Литература

• Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.

Ссылки

• Moebius Transformations Revealed на Преобразования Мебиуса — наглядное объяснение (с русскими субтитрами) на YouTube.