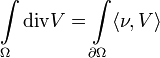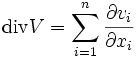Остроградского формула

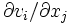Теорема Остроградского — Гаусса — утверждение интегрального исчисления функций многих переменных, устанавливающее связь между n-кратным интегралом по области и (n − 1)-кратным интегралом по её границе. Пусть V = (v₁,v₂,...,v_n) есть векторное поле на $\R^n$, такое что функции v_i вместе со своими частными производными $\partial v_i/ \partial x_j$ интегрируемы по Лебегу в ограниченной области Ω, граница 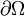$\partial\Omega$ которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.

Тогда формула Остроградского имеет вид

$\int\limits_\Omega \operatorname{div} V=\int\limits_{\partial \Omega}\langle\nu,V\rangle$

где

$\operatorname{div} V=\sum_{i=1}^n\frac{\partial v_i}{\partial x_i}$

есть дивергенция поля V.

---

Формула Остроградского — Гаусса в векторной форме имеет вид

$\iiint\limits_T \mathrm{div}\mathbf{F} dV = \oint \limits_S \mathbf{ F n} dS$,

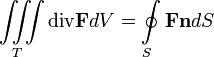то есть интеграл от дивергенции векторного поля 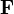${\mathbf F}$, распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по поверхности, ограничивающей данный объём, то есть замкнутых, таких как поверхность воздушного шарика, и не применима к поверхностям, таким как воздушный шар с подогревом.

В работе Остроградского формула записана в следующем виде,

$\int \left( \frac{dp}{dx} + \frac{dq}{dy} +\frac{dr}{dz} \right) \omega = \int (P \cos \lambda + Q \cos \mu + R \cos \nu ) s$,

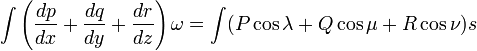где ω и s дифференциалы объёма и поверхности. В современной записи ω = dΩ — элемент объема, s = dS — элемент поверхности. 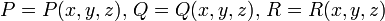$P = P(x,y,z),\,Q=Q(x,y,z),\, R=R(x,y,z)$ — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

История

Для гладких функций эта формула была впервые получена в трёхмерном случае Остроградским в 1828 (опубликована в 1831). На n-мерный случай была обобщена им же в 1834 (опубликовано в 1838). С помощью этой формулы Остроградский нашёл выражение производной по параметру от n-кратного интеграла с переменными пределами и получил формулу для вариации n-кратного интеграла. При n = 3 для одного частного случая формула Остроградского была получена Гауссом в 1813, поэтому иногда она называется также формулой Остроградского — Гаусса. Что интересно, в западной литературе порядок фамилий изменён — она именуется как «теорема Гаусса — Остроградского». Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

Литература

• Остроградский М. В., Note sur les integrales definies. Mem. 1’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
• Остроградский М. В., Memoire sur le calcul des variations des integrales multiples. Mem. 1’Acad., 1, стр. 35—58, 24/1 1834 (1838)