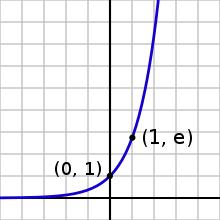
Показательная функция

Показательная функция — математическая функция $f(x) = a^x\,\!$, где $a$ называется основанием степени, а $x$ — показателем степени.

• В вещественном случае основание степени $a\,\!$ — некоторое неотрицательное вещественное (действительное) число, а аргументом функции является вещественный показатель степени.
• В теории комплексных функций рассматривается более общий случай, когда аргументом и показателем степени может быть произвольное комплексное число.
• В самом общем виде — $u^v$, введена Лейбницем в 1695 г.

Особо выделяется случай, когда в качестве основания степени выступает число e. Такая функция называется экспонентой (вещественной или комплексной).

Вещественная функция

Определение показательной функции

Пусть $a$ — неотрицательное вещественное число, $x$ — рациональное число: $x=\frac{m}{n}$. Тогда $a^x\,\!$ определяется по следующим правилам.

• Если $x>0$, то $a^x=\sqrt[n]{a^m}$.
• Если $x=0$ и $a \ne 0$, то $a^x=1\,\!$.
  • Значение $0^0$ не определено (см. Раскрытие неопределённостей).
• Если $x<0$ и $a>0$, то $a^x=\frac {1} {a^{|x|}}$.
  • Значение $a^x$ при $x<0, a=0$ не определено.

Для произвольного вещественного показателя $x$ значение $a^x$ можно определить как предел последовательности $a^{r_n}$, где $r_n$ — рациональные числа, сходящиеся к $x$. Для экспоненты есть и другие определения через предел, например:

$e^x = \lim_{n \rightarrow \infty} \left(1 + \frac{x}{n}\right)^{n}.$

Свойства

График экспоненты

• $a^0 = 1\,\!$
• $a^{x+y} = a^x \, a^y$
• $(a^x)^y = a^{xy}\,\!$
• $(ab)^x = a^x \, b^x$

Используя функцию натурального логарифма $\ln \, x$, можно выразить показательную функцию с произвольным положительным основанием через экспоненту:

$a^x = e^{x\cdot \ln a}$

Эта связь позволяет ограничиться изучением свойств экспоненты.

Аналитические свойства:

${d \over dx} a^x = (\ln a) a^x.$

В частности:

$\,{d \over dx} e^x = e^x$

Доказательство  

I. Докажем, что ${d \over dx} e^x = e^x$

$\lim_{\Delta x \to 0} \frac {e^{x+\Delta x}-e^x} {\Delta x} = \lim_{\Delta x \to 0} \frac {e^x \cdot (e^{\Delta x}-1)} {\Delta x} = e^x \cdot \lim_{\Delta x \to 0} \frac {e^{\Delta x} - 1} {\Delta x} = e^x \cdot 1 = e^x$. Ч. т. д.

Докажем, что $\lim_{\Delta x \to 0} \frac {e^{\Delta x} - 1} {\Delta x} = 1$. Пусть $e^{\Delta x} - 1 = u$, тогда $e^{\Delta x}=u+1 \Rightarrow \Delta x = \ln (u+1)$. Если $\Delta x \to 0$, то $u = e^{\Delta x} - 1 \to 0$

$\lim_{\Delta x \to 0} \frac {e^{\Delta x} - 1} {\Delta x} = \lim_{u \to 0} \frac {u} {\ln (u+1)} = \lim_{u \to 0} \frac {1} {\frac {1} {u} \ln (u+1)} = \lim_{u \to 0} \frac {1} {\ln (u + 1)^{\frac {1} {u} }} = \frac {\lim_{u \to 0} 1} {\lim_{u \to 0} \ln (u+1)^{\frac {1} {u}}} = \frac {1} {\ln \lim_{u \to 0} (u+1)^{\frac {1} {u}}} = \frac {1} {\ln e} = 1.$

II. ${d \over dx} a^x = {d \over dx} \left (e^{\ln a} \right )^x = {d \over dx} e^{x \cdot \ln a} = e^{x \cdot \ln a} \cdot \ln a = a^x \cdot \ln a$ Ч. т. д.

Разложение в ряд:

$e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots$.

Асимптотика

Показательная функция растёт на бесконечности быстрее любой полиномиальной:

$\lim\limits_{x\to \infty}\frac{x^n}{a^x}=0$

Большая скорость роста может быть проиллюстрирована, например, задачей о складывании бумаги.

Комплексная функция

Для расширения экспоненты на комплексную плоскость определим её с помощью того же ряда, заменив вещественный аргумент на комплексный:

$e^z = \sum_{n = 0}^{\infty} {z^n \over n!} = 1 + z + {z^2 \over 2!} + {z^3 \over 3!} + {z^4 \over 4!} + \cdots$

Эта функция имеет те же основные алгебраические и аналитические свойства, что и вещественная. Отделив в ряде для $e^{ix}$ вещественную часть от мнимой, мы получаем знаменитую формулу Эйлера:

$~e^{ix}=\cos x+i\sin x$

Таким образом, комплексная экспонента периодична вдоль мнимой оси.

Показательная функция с произвольным комплексным основанием и показателем степени легко вычисляется с помощью комплексной экспоненты и комплексного логарифма.

Пример: $i^i=e^{i~\ln(i)}$; поскольку $\ln (i) = i \frac{\pi} {2}$ (главное значение логарифма), окончательно получаем: $i^i = e^{i \frac{i \pi} {2}} = e^{- \frac{\pi} {2}}$.

См. также

• Возведение в степень
• Ограничение складывания бумаги пополам
• Степенная функция
• Экспонента

Литература

• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, тома I, II. — М.: ФИЗМАТЛИТ, 2001. — ISBN 5-9221-0156-0, 5-9221-0155-2