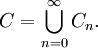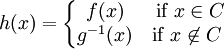- Теорема Кантора — Бернштейна
-
Теорема Кантора — Бернштейна
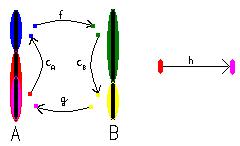
Теорема Кантора — Бернштейна (в англ. литературе теорема Кантора — Бернштейна — Шрёдера), утверждает, что если существуют инъективные отображения
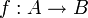 и
и 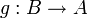 между множествами A и B, то существует взаимооднозначное отображение
между множествами A и B, то существует взаимооднозначное отображение 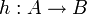 . Другими словами, что мощности множеств A и B совпадают:
. Другими словами, что мощности множеств A и B совпадают:- | A | = | B | .
Неформально говоря, теорема утверждает следующее:
Из
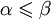 и
и 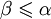 , следует, что α = β.
, следует, что α = β.Утверждение теоремы является очевидным, если под α и β подразумеваются действительные числа, однако теорема ведёт речь о кардинальных числах.
Содержание
Доказательство
Пусть
и
и
Тогда, для любого
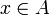 положим
положимЕсли x не лежит в C, тогда x должен быть в g[B] (образе множества B под действием отображения g). И тогда существует g − 1(x), и h корректно определённое взаимооднозначное отображение (биекция).
Можно проверить, что
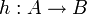 и есть искомое взаимооднозначное отображение.
и есть искомое взаимооднозначное отображение.Заметим, что это определение отображения h неконструктивно в том смысле, что не существует общего алгоритма определения за конечное число шагов для любых заданных множеств A, B и инъекций f, g, лежит ли некоторый элемент x множества A в множестве C или нет. Хотя для некоторых частных случаев, такой алгоритм существует.
История
Теорема названа в честь Георга Кантора, Феликса Бернштейна и Эрнста Шрёдера
Первоначальное доказательство использовало аксиому выбора, однако эта аксиома необязательна для доказательства данной теоремы.
Эрнст Шрёдер первым сформулировал теорему, но опубликовал неправильное доказательство. Независимо эта теорема была сформулирована Кантором. Ученик Кантора Феликс Бернштейн опубликовал диссертацию, содержащую полностью корректное доказательство.
См. также
- Эрнст Шрёдер
- Георг Кантор
- Феликс Бернштейн
- Теория множеств
- Кардинальное число
Литература
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004. — 336 с.
Wikimedia Foundation. 2010.
Теорема Кантора (значения) — Теорема Кантора: Теорема Кантора о множестве подмножеств в теории множеств Теорема Кантора Бендиксона Теорема Кантора Бернштейна Теорема Кантора Гейне … Википедия
Теорема Кантора-Бернштейна-Шредера — … Википедия
Теорема Кантора-Бернштейна-Шрёдера — … Википедия
КАНТОРА ТЕОРЕМА — 1) Множество 2A, состоящее из всех подмножеств множества А, не равномощно ни самому А, ни его подмножеству. Идея доказательства этой теоремы, принадлежащая Г. Кантору (G.Cantor, 1878), получила название канторова диагонального метода и играет… … Математическая энциклопедия
Кантор, Георг Фердинанд Людвиг Филипп — В Википедии есть статьи о других людях с такой фамилией, см. Кантор. Георг Кантор Georg Ferdinand Ludwig Philipp Cantor … Википедия
Кантор, Георг — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург … Википедия
Кантор, Георг Фердинанд — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург … Википедия
Кантор Георг — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург … Википедия
Кантор Георг Фердинанд — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург … Википедия
Кантор Георг Фердинанд Людвиг Филипп — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург … Википедия

![C_0=A\setminus g[B],\!](http://dic.academic.ru/pictures/wiki/files/56/8cee0cfc4586b198cd8d03c5a22702bd.png)
![C_{n+1}=g[f[C_n]]\quad \mbox{ for }n\geqslant 0](http://dic.academic.ru/pictures/wiki/files/101/e3ec3f0e7abfbcf4517fcd7b905d7d1f.png)