- Метод минимального элемента
-
Транспортная задача — задача об оптимальном плане перевозок продукта (-ов) из пунктов отправления в пункты потребления. Разработка и применение оптимальных схем грузовых потоков позволяют снизить затраты на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной или входит в класс сложности NP. Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной.
Содержание
Постановка задачи
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).
История поиска методов решения
Задача о максимальном потоке в сети изучается уже более 60 лет. Интерес к ней подогревается огромной практической значимостью этой проблемы. Методы решения задачи применяются на транспортных, коммуникационных, электрических сетях, при моделировании различных процессов физики и химии, в некоторых операциях над матрицами, для решения родственных задач теории графов и даже для поиска Web-групп в WWW. Исследования данной задачи проводятся во множестве крупнейших университетов мира.
60 лет назад эта задача решалась симплекс-методом линейного программирования, что было крайне неэффективно. Форд и Фалкресон предложили рассматривать для решения задачи о максимальном потоке ориентированную сеть и искать решение с помощью итерационного алгоритма. В течение 20 лет все передовые достижения в исследовании данной задачи базировались на их методе.
В 1970 году Диниц предложил решать задачу с использованием вспомогательных бесконтурных сетей и псевдомаксимальных потоков, что намного увеличило быстродействие разрабатываемых алгоритмов. В 1974 году Карзанов улучшил метод Диница, введя такое понятие как предпоток. Алгоритмы Диница и Карзанова, как и исследования Форда и Фалкерсона, внесли огромный вклад в решение данной проблемы. На основе их методов 15 лет достигались наилучшие оценки быстродействия алгоритмов.
В 1986 году появился третий метод, который также без раздумий можно отнести к фундаментальным. Этот метод был разработан Голдбергом и Таряном, и получил название Push-Relabel метода. Для нахождения максимального потока он использует предпотоки и метки, изменяемые во время работы алгоритма. Push-Relabel алгоритмы очень эффективны и исследуются до сих пор.
В 1997 году Голдберг и Рао предложили алгоритм, присваивающий дугам неединичную длину. Это один из самых современных алгоритмов. Асимптотическая оценка его быстродействия превзошла
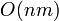 , о такой скорости многие годы можно было только мечтать. Затем алгоритм Голдберга и Рао тщательно изучался и улучшался.
, о такой скорости многие годы можно было только мечтать. Затем алгоритм Голдберга и Рао тщательно изучался и улучшался.Методы решения
Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей ее можно решить проще (для задач малой размерности).
Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из
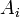 в
в 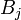 груза
груза 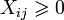 , а в маленькие клетки — соответствующие тарифы
, а в маленькие клетки — соответствующие тарифы 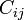 .
.Затем требуется определить опорный план и путем последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимацией Фогеля.
Метод северо-западного угла (диагональный). На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из
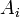 или полностью удовлетворяется потребность
или полностью удовлетворяется потребность 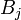 .
.Одним из способов решения задачи является метод минимального (наименьшего) элемента Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.
Алгоритм решения:
- Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают меньшее из чисел.
- Проверяются строки поставщиков на наличии строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.
- Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п.1, в противном случае задача решена.
Затем рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления - в нижней. Пункты производства и потребления попарно соединяются рёбрами бесконечной пропускной способности и цены за единицу потока
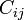 .
.К верхней доле искусственно присоединяется исток. Пропускная способность рёбер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих рёбер равна 0.
Аналогично к нижней доле присоединяется сток. Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.
Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Её решение аналогично нахождению максимального потока в алгоритме Форда—Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешёвый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана—Форда. При возврате потока стоимость считается отрицательной.
Алгоритм mincost maxflow можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма mincost maxflow происходит не более чем за
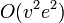 операций. (
операций. ( — количество рёбер,
— количество рёбер, 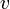 — количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка
— количество вершин.) При случайно подобраных данных обычно требуется гораздо меньше — порядка 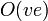 операций.
операций.При решении несбалансированную транспортной задачи, применяют прием, позволяющий сделать ее сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.
Ссылки
Wikimedia Foundation. 2010.
