Метод деформируемого многогранника

Последовательные симплексы в методе Нелдера-Мида для функции Розенброка (англ.) (вверху) и функции Химмельблау (англ.) (внизу)

Не путать с «симплекс-методом» из линейного программирования — методом оптимизации линейной системы с ограничениями.

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в генетическом методе отжига.

Алгоритм

Пусть требуется найти безусловный минимум функции n переменных 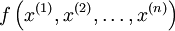$f\left(x^{(1)},x^{(2)},\ldots,x^{(n)}\right)$. Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

• коэффициент отражения α > 0, обычно выбирается равным 1.
• коэффициент сжатия β > 0, обычно выбирается равным 0,5.
• коэффициент растяжения γ > 0, обычно выбирается равным 2.

Подготовка. Вначале выбирается n + 1 точка 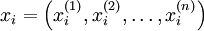$x_i = \left(x^{(1)}_i,x^{(2)}_i,\ldots,x^{(n)}_i\right)$, образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: $f_1=f(x_1), f_2=f(x_2),\ldots, f_{n+1}=f(x_{n+1})$.

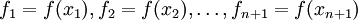Дальнейший план действий:

1. Сортировка. Из вершин симплекса выбираем три точки: x_h с наибольшим (из выбранных) значением функции f_h, x_g со следующим по величине значением f_g и x_l с наименьшим значением функции f_l. Целью дальнейших манипуляций будет уменьшение по крайней мере f_h.

2. Найдём центр тяжести всех точек, за исключением x_h: 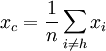$x_c=\frac{1}{n}\sum\limits_{i\neq h} x_i$. Вычислять f_c = f(x_c) не обязательно.

3. Отражение. Отразим точку x_h относительно x_c с коэффициентом α (при α = 1 это будет центральная симметрия, в общем случае — гомотетия), получим точку x_r и вычислим в ней функцию: f_r = f(x_r). Координаты новой точки вычисляются по формуле:

x_r = (1 + α)x_c − αx_h

4. Далее смотрим, насколько нам удалось уменьшить функцию, ищем место f_r в ряду f_h,f_g,f_l:

4а Если f_r < f_l, то направление выбрано удачное и можно попробовать увеличить шаг — производим растяжение. Новая точка x_e = (1 − γ)x_c + γx_r и значение функции f_e = f(x_e).

• Если f_e < f_l, то можно расширить симплекс до этой точки: заменяем точку x_h на x_e и заканчиваем итерацию (на шаг 8).

  Если f_e > f_l, то переместились слишком далеко: в набор берём x_r (опять вместо x_h) и заканчиваем итерацию (на шаг 8).

4b Если f_l < f_r < f_g, то выбор точки уже неплохой (новая лучше двух прежних). Заменяем точку x_h на x_r и переходим на шаг 8.

4с Если f_h > f_r > f_g, то меняем обозначения x_r,x_h (и соответствующие значения функции) местами и идём на шаг 5.

4d Если f_r > f_h, то просто идём на следующий шаг 5.

В результате (возможно, после переобозначения) f_r > f_h > f_g > f_l.

5. Сжатие. Строим точку x_s = βx_h + (1 − β)x_c и вычисляем в ней значение f_s.

6 Если f_s < f_h, то заменяем точку x_h на x_s и идём на шаг 8.

7 Если f_s > f_h, то первоначальные точки оказались самыми маленькими. Делаем глобальное сжатие симплекса — гомотетию к точке с наименьшим значением x₀:

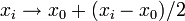$x_i \to x_0 + (x_i-x_0)/2$ для всех требуемых точек x_i.

8 Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

См. также

• Метод сопряжённых градиентов
• Алгоритм имитации отжига

Источники

• КУРС «Многомерная оптимизация». Лекция 10. Метод Нелдера-Мида на сайте ИНТУИТа. Подробное описани, есть иллюстрации.
• Метод Нелдера-Мида. Краткий алгоритм.
• Список ссылок на численные методы
• J.A. Nelder and R. Mead, Computer Journal, 1965, vol 7, pp 308—313 [1] (текст не общедоступен)(англ.)