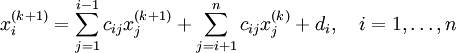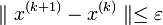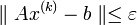- Метод Гаусса-Зейделя
-
Метод Гаусса—Зейделя[1] является классическим итерационным методом решения системы линейных уравнений.
Содержание
Постановка задачи
Возьмём систему:
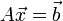 , где
, где 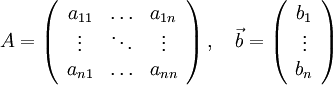
Или
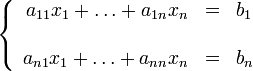
И покажем, как её можно решить с использованием метода Гаусса-Зейделя.
Метод
Чтобы пояснить суть метода, перепишем задачу в виде:
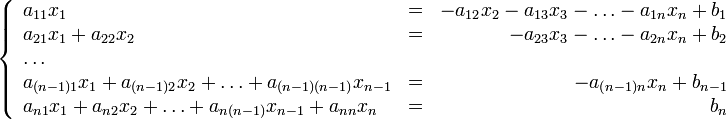
Здесь в j-м уравнении мы перенесли в правую часть все члены, содержащие xi , для i > j. Эта запись может быть представлена:
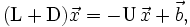
где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули.
Итеративный процесс в методе Гаусса-Зейделя строится по формуле
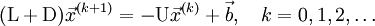 после выбора соответствующего начального приближения
после выбора соответствующего начального приближения 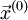 .
.Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения
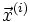 используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации: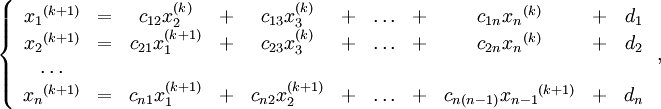
где
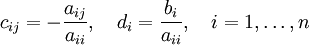
Таким образом i-тая компонента (k + 1)-го приближения вычисляется по формуле:
Условие сходимости
Приведем достаточное условие сходимости метода.

Теорема.
Пусть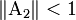 , где
, где 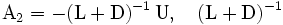 – матрица, обратная к
– матрица, обратная к 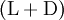 . Тогда при любом выборе начального приближения
. Тогда при любом выборе начального приближения 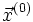 :
:
- метод Гаусса-Зейделя сходится;
- скорость сходимости метода равна скорости сходимости геометрической прогрессии со знаменателем
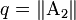 ;
; - верна оценка погрешности:
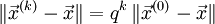 .
.
Условие окончания
Условие окончания итерационного процесса Зейделя при достижении точности
 в упрощённой форме имеет вид:
в упрощённой форме имеет вид:Более точное условие окончания итерационного процесса имеет вид
и требует больше вычислений. Хорошо подходит для разреженных матриц.
Пример алгоритма на с++
// Условие сходимости bool converge(double *xk, double* xkp) { bool b = true; for (int i = 0; i < n; i++) { if (fabs(xk[i]-xkp[i]) > eps) { b = false; break; } } return b; } while(converge(x,p)) { for(int i = 0; i < n; i++) { var = 0; for(int j = 0; j < n; j++) { if(j != i){ var += (a[i][j]*x[j]); } } p[i] = x[i]; x[i]=(b[i] - var)/a[i][i]; } }
Примечания
- ↑ Людвиг Зейдель (1821—1896) — немецкий астроном и математик, Карл Фридрих Гаусс (1777—1855) — немецкий математик, астроном и физик
См. также
Wikimedia Foundation. 2010.