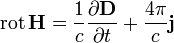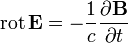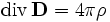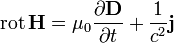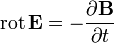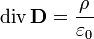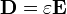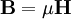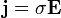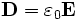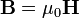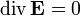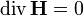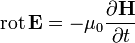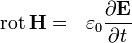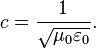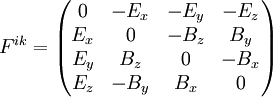Максвелла уравнения

Классическая электродинамика

Магнитное поле соленоида

Электричество · Магнетизм Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Электродинамика Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-ток · 4-потенциал Известные учёные Генри Кавендиш Майкл Фарадей Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

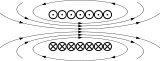
Уравнения Максвелла — основные уравнения классической электродинамики, описывающие эволюцию электромагнитного поля и его взаимодействие с зарядами и токами. Уравнения были опубликованы Дж. К. Максвеллом в 1873 году в его книге «Трактат об электричестве и магнетизме».

Уравнения в классическом виде

Уравнения в общем виде

Название	Дифференциальная форма	Интегральная форма	Примерное словесное выражение
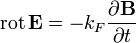
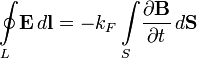
Закон индукции Фарадея	$\operatorname{rot}\,\mathbf{E} = - k_F{\partial \mathbf{B} \over \partial t}$	$\oint\limits_L\!\mathbf{E}\, d\mathbf{l} = - k_F \int\limits_S\!{\partial \mathbf{B} \over \partial t}\, d\mathbf{S}$	Изменение магнитной индукции порождает вихревое электрическое поле
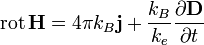
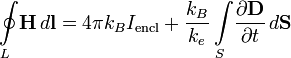
Закон Ампера (с добавкой от Максвелла)	$\operatorname{rot}\,\mathbf{H} = 4\pi k_B\mathbf{j} + {k_B \over k_e} {\partial \mathbf{D} \over \partial t}$	$\oint\limits_L\!\mathbf{H}\, d\mathbf{l} = 4\pi k_B I_{\mathrm{encl}} + {k_B \over k_e} \int\limits_S\!{\partial \mathbf{D} \over \partial t}\, d\mathbf{S}$	Электрический ток и изменение электрической индукции порождают вихревое магнитное поле
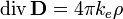
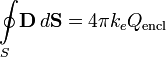
Теорема Гаусса	$\operatorname{div}\,\mathbf{D} = 4 \pi k_e \rho$	$\oint\limits_S\!\mathbf{D}\, d\mathbf{S} = 4 \pi k_e Q_{\mathrm{encl}}$	Электрический заряд является источником электрической индукции
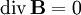
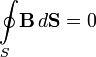
Теорема Гаусса	$\operatorname{div}\,\mathbf{B} = 0$	$\oint\limits_S\!\mathbf{B}\, d\mathbf{S} = 0$	Магнитная индукция не расходится (не имеет источников). (Неприменима к монополям. До сих пор монополей в природе не обнаружено.)

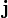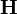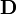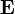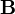Приведенные выше уравнения Максвелла не составляют еще полной системы уравнений электромагнитного поля, поскольку они не содержат свойства среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины $\mathbf{j}$, $\mathbf{H}$, $\mathbf{D}$, $\mathbf{E}$ и $\mathbf{B}$, в которых учитываются индивидуальные свойства среды, называются материальными уравнениями.

Введённые обозначения:

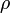• $\rho \$ — плотность стороннего электрического заряда (в единицах СИ — Кл/м³)
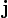• $\mathbf j$ — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²)
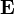• $\mathbf E$ — напряжённость электрического поля (в единицах СИ — В/м)
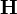• $\mathbf H$ — напряжённость магнитного поля (в единицах СИ — А/м)
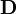• $\mathbf D$ — электрическая индукция (в единицах СИ — Кл/м²)
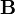• $\mathbf B$ — магнитная индукция (в единицах СИ — Тл = Вб/м²= кг·с^-2·А^-1)
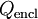• $Q_{\mathrm{encl}} \$ — сторонний электрический заряд, заключенный внутри поверхности 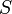$S \$ (в единицах СИ — Кл)
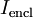• $I_{\mathrm{encl}} \$ — электрический ток, проходящий через поверхность 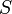$S \$ вызванный движением свободных зарядов (в единицах СИ — А)

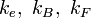• $k_e,\ k_B,\ k_F$ — коэффициенты, зависящие от системы единиц.

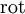• $\mathrm{rot} \$ — дифференциальный оператор ротора
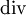• $\mathrm{div} \$ — дифференциальный оператор дивергенции
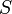• $S\$ — замкнутая двумерная поверхность
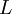• $L\$ — замкнутый контур

Уравнения в Гауссовой системе единиц

$\operatorname{rot}\,\mathbf{H} = {1 \over {c}} {\partial \mathbf{D} \over \partial t} + {4\pi \over {c}}\mathbf{j}$

$\operatorname{rot}\,\mathbf{E} = - {1 \over {c}} {\partial \mathbf{B} \over \partial t}$

$\operatorname{div}\,\mathbf{D} = 4\pi\rho$

$\operatorname{div}\,\mathbf{B} = 0$

Уравнения в системе СИ

$\operatorname{rot}\,\mathbf{H} = \mu_0 {\partial \mathbf{D} \over \partial t} + {1 \over {c^2}}\mathbf{j}$

$\operatorname{rot}\,\mathbf{E} = - {\partial \mathbf{B} \over \partial t}$

$\operatorname{div}\,\mathbf{D} = {\rho \over \varepsilon_0}$

$\operatorname{div}\,\mathbf{B} = 0$

Материальные уравнения

Чтобы дополнить уравнения Максвелла до полной системы уравнений электродинамики, необходимо получить материальные уравнения, которые связывают величины 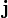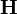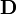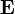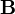$\mathbf{j}$, $\mathbf{H}$, $\mathbf{D}$, $\mathbf{E}$, $\mathbf {B}$ и в которых учтены индивидуальные свойства среды. Способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электропроводности среды. В основе таких теорий лежат в той или иной степени идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами 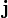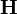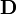$\mathbf{j}$, $\mathbf{H}$, $\mathbf{D}$ с одной стороны и 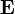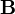$\mathbf{E}$, $\mathbf{B}$ с другой стороны. В случае слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени, а также для изотропных, неферромагнитных и несегнетоэлектрических сред материальные уравнения записываются в виде:

$\mathbf{D} = \varepsilon\mathbf{E}$

$\mathbf{B} = \mu\mathbf{H}$

$\mathbf{j} = \sigma\mathbf{E}$

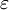где $\varepsilon \$ — диэлектрическая проницаемость (в единицах СИ — Ф/м), 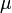$\mu \$ — магнитная проницаемость (в единицах СИ — Гн/м) и 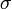$\sigma \$ — электропроводность среды (в единицах СИ — 1/(Ом·м)).

В вакууме, без зарядов и токов

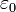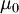Вакуум — это линейная, однородная, изотропная, бездисперсионная среда; и магнитная, и электрическая постоянные обозначаются через $\varepsilon_0 \$ и $\mu_0 \$ (не учитывая очень малых квантовых эффектов).

$\mathbf{D} = \varepsilon_0 \mathbf{E}$

$\mathbf{B} = \mu_0 \mathbf{H}$

Уравнения Максвелла для вакуума без электрических зарядов и токов такие:

$\mathrm{div}\, \mathbf{E} = 0$

$\mathrm{div}\, \mathbf{H} = 0$

$\mathrm{rot}\, \mathbf{E} = - \mu_0 \frac{\partial\mathbf{H}} {\partial t}$

$\mathrm{rot}\, \mathbf{H} = \ \ \varepsilon_0 \frac{\partial \mathbf{E}} {\partial t}$

Эта система дифференциальных уравнений имеет простое решение — гармоническая, плоская волна. Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу, и находятся в фазе. Волна распространяется со скоростью:

$c = \frac{1}{\sqrt{\mu_0 \varepsilon_0}}.$

Максвелл обозначил эту величину c. Это просто скорость света в вакууме, а свет — это вид электромагнитного излучения. Общепринятые значения^[1] скорости света, электрической и магнитной постоянных приведены в следующей таблице:

Символ	Имя	Численное значение	Единицы измерения СИ	Тип
$c \$	Постоянная скорости света	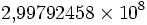$2{,}99792458 \times 10^8$	м/с	LT−1
$\ \varepsilon_0$	Электрическая постоянная	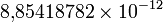$8{,}85418782 \times 10^{-12}$	Ф / м	L−3M−1T4I²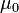
$\ \mu_0 \$	Магнитная постоянная	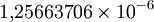$1{,}25663706 \times 10^{-6}$	Гн / м	LMT−2I−2

Релятивистская инвариантность

Уравнения Максвелла в вакууме инвариантны относительно преобразований Лоренца. Это послужило одним из толчков к созданию специальной теории относительности. В ковариантной форме уравнения приобретают вид (в системе единиц СГС):

$\partial_i F^{i k} = \frac{4\pi}{c} J^k \,$

$\partial_i F_{k l} + \partial_k F_{l i} + \partial_l F_{i k} = 0 \,$,

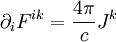
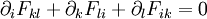где 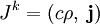$J^k=(c\rho,\; \mathbf{j})$ — 4-ток, а 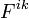$\ F^{i k}$ — антисимметричный тензор электромагнитного поля:

$F^{i k} = \left( \begin{matrix} 0 & -E_x & -E_y & -E_z \\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix} \right)$

Примечания

1. ↑ Значения физических постоянных

Литература

• Матвеев А. Н. Электричество и магнетизм. М.: Высшая школа, 1983.
• Тоннела М.-А. Основы электромагнетизма и теории относительности. Пер. с фр. М.: Иностранная литература, 1962. 488 с.
• Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
• Фущич В. И., Никитин А. Г., Симметрия уравнений Максвелла. Киев: Наук. думка, 1983. 200 с.

См. также

• Фундаментальные физические постоянные
• Уравнения Джефименко