ШВАРЦШИЛЬДА ПРОСТРАНСТВО-ВРЕМЯ

ШВАРЦШИЛЬДА ПРОСТРАНСТВО-ВРЕМЯ

-пространство-время вне массивного невращающегося тела в вакууме (тензор Риччи R_ik = 0). Элемент длины ds определяется выражением

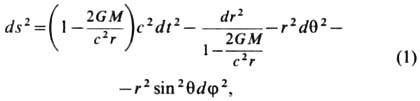
где r,q, f - сферические координаты с центром в центре массивного тела, M - масса тела. Это решение ур-ний Эйнштейна общей теории относительности было найдено К. Шварцшильдом (К. Schwarzschild, 1916). Величина r_q =2GМ/с². наз. радиусом Шварцшильда или гравитационным радиусом. Ш. п.-в. является асимптотически плоским при r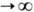. и обладает там правильной ньютоновской асимптотикой: 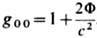, где 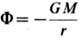-ньютоновский гравитационный потенциал.

На поверхности массивного тела метрика Ш. <п.-в. (1) должна непрерывно сшиваться с метрикой, описывающей пространство-время внутри тела. При этом радиальная координата поверхности тела в Ш. п.-в. должна быть больше r_q, иначе равновесие тела невозможно. Ш. п.-в. имеет смысл и в отсутствие центрального тела. Тогда его можно аналитически продолжить под гравитационный радиус, в область r<r_q, используя др. системы отсчёта [Д. Финкель-штейн (D. Finkelstein), 1958]. Поверхность r = r_q является изотропной, так что все массивные или безмассовые частицы могут пересекать её только в одну сторону (из-за этого её также называют горизонтом). Если граничные условия при r = r_q таковы, что частицы пересекают гравитационный радиус в сторону уменьшения r, то Ш. <п.-в. описывает чёрную дыру, образовавшуюся в результате коллапса первоначально регулярного распределения материи (напр., звезды), и тогда поверхность r = r_q является горизонтом событий. В противном случае Ш. <п.-в. содержит белую дыру. В области под гравитационным радиусом частицы могут двигаться либо только в сторону уменьшения r в случае чёрной дыры, либо только в обратную сторону в случае белой дыры. Максимальное аналитическое продолжение Ш. <п.-в. в отсутствие вещества [M. Крускал (M. Kruskal), 1960] содержит и чёрную, и белую дыры (внутри каждой из к-рых находится поверхность r =0),

а также две несвязанные пространственные асимптотически-плоские бесконечности r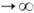. Однако такое максимальное расширение Ш. п.-в. не является физическим в том смысле, что оно не может возникнуть как результат динамической эволюции регулярного распределения материи. Его тензор кривизны конечен и регулярен при r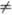0. Две несвязанные поверхности r =0, на к-рых он расходится, есть 3-мерные пространственноподобные гиперповерхности. Поэтому нельзя сказать, что r =0есть "центр" Ш. п.-в., в отличие от случая центрального тела с радиусом r₀>r_q.

Можно доказать, что Ш. <п.-в.- единственное статическое вакуумное асимптотически-плоское решение ур-ний общей теории относительности. Ш. п.-в., описывающее чёрную дыру, устойчиво: малые возмущения метрики (1) общего вида затухают по степенному закону при t 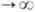(показатель степени определяется мультипольностью возмущения). Гравитационная энергия связи тел массой т<<М, двигающихся по устойчивым круговым орбитам в Ш. <п.-в., может достигать 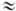6% от энергии покоя (С. А. Каплан, 1949). Частицы, падающие в чёрную дыру, достигают поверхности горизонта событий за конечное собственное время ~r_q/с, но за бесконечный интервал времени t с точки зрения любого внеш. наблюдателя, не падающего в чёрную дыру. Это утверждение остаётся верным и в случае нестационарной чёрной дыры, масса к-рой растёт из-за поглощения ( аккреции )ею окружающего вещества [при этом, однако, следует помнить, что в случае аккреции на чёрную дыру радиус поверхности горизонта событий r_h,(t )всегда несколько больше текущего гравитационного радиуса r_q(t)]. После пересечения горизонта событий частицы достигают сингулярности r = 0 также за конечный интервал собственного времени. Внеш. наблюдатель этого не увидит никогда.

Лит.: Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; Хокинг С., Эллис Дж., Крупномасштабная структура пространства-времени, пер. с англ., M., 1977.

А. А. Старобинский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.