БРАУЭРА РЕШЕТКА

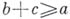Брауэра структура, Брауэра алгебра, - дистрибутивная решетка, в к-рой для каждой пары элементов а, b существует элемент, наз. псевдоразностью (часто обозначаемый через ), являющийся наименьшим среди элементов ссо свойством . Возможно эквивалентное описание Б. р. как многообразия универсальных алгебр с тремя бинарными операциями удовлетворяющими нек-рым аксиомам. Термин "Брауэра алгебра" был введен ввиду наличия связи Б. р. с интуиционистской логикой Брауэра (L. Е. J. Brouwer). Чаще-.вместо Б. р. используются так наз. псевдобулевы алгебры, теория к-рых двойственна тебрии Б. р. Любая Б. р. превращается в псевдобулеву алгебру при введении нового порядка , новых объединений и пересечений по формулам и операции относительного псевдодополнения 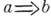, совпадающей с псевдоразностью 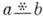. Обратно, любая псевдобулева алгебра может быть-рассматриваема как Б. р. Иногда термин "Б. р." используется для псевдобулевых алгебр (см., напр., [2]).

Лит.:[1] Мас Кinsеу J. С. С., Таrski A., "Ann. Math.", 1944, v. 45, p. 141-91; [2] Биркгоф Г., Теория структур, пер. с англ., М., 1952. В. А. Янков.