БИВЕКТОР

БИВЕКТОР

- упорядоченная пара векторов аффинного пространства отложенных от общего начала. Б. полагается равным нулю, если составляющие его векторы 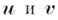коллинеарны. Ненулевой Б. определяет в Анесущую его двумерную плоскость. Два Б. наз. параллельными, если параллельны несущие их плоскости. Если пространство имеет конечную размерность - контравариантныё координаты вектора -контравариантныё координаты вектора 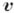, вычисленные в нек-ром базисе пространства A, то величины


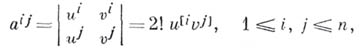
наз. координатами бивектора в базисе е. Эти координаты кососимметричны по своим индексам; среди них существенных координат. При переходе в A к другому базису координаты Б. ведут себя как координаты дважды контравариантного тензора. Два Б. наз. равными, если в к.-л. базисе равны их координаты (они будут равны и в любом другом базисе). Класс равных Б. наз. свободным бивектором. При наличии в Аскалярного произведения на Б. распространяется ряд метрич. понятий векторной алгебры. Мерой Б. наз. площадь параллелограмма, образованного векторами 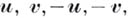начало каждого из к-рых помещено в конец предыдущего. Равные Б. имеют равную меру. Скалярным произведением двух Б. наз. число, равное произведению мер сомножителей на косинус угла между несущими их плоскостями. Скалярное произведение является билинейной формой от координат сомножителей, коэффициенты к-рой определяются только метрич. тензором пространства А.

Если размерность Аравна 3, то Б. может быть отождествлен с вектором пространства А, наз. векторным произведением векторов

В тензорном исчислении Б. наз. любой контравариантный кососимметрический тензор валентности 2 [т. е. тензор типа (2,0)]. Каждый такой тензор может быть представлен в виде суммы тензоров, к-рым соответствуют ненулевые Б. с различными несущими плоскостями. Они определяют листы бивектора. Ранг косоеимметрической матрицы размера , составленной из координат В., есть четное число

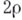, где - число листов Б. В пространстве Анад полем действительных чисел эта матрица подобна матрице


с блоками


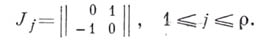
См. также Внешнее произведение, Поливектор, Плюккеровы координаты.

Лит.:[1] Схоутен Я. А.. Тензорный анализ для физиков, пер. с англ., М., 1965. Л. Я. Купцов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "БИВЕКТОР" в других словарях:

  • Бивектор — Поливектор, р вектор, векторного пространства V элемент некоторой внешней степени Λp пространства V над полем k. p вектор может пониматься как кососимметризованный р раз контравариантный тензор на V. 2 вектор также называют бивектором. Свойства… …   Википедия

  • БИВЕКТОРНОЕ ПРОСТРАНСТВО — центроаффинное пространство к рое может быть отнесено каждой точке пространства аффинной связности (в частности, риманова пространства ). Пусть в точке пространства (или ) рассматриваются все тензоры, у к рых ковариантная и контравариантная… …   Математическая энциклопедия

  • Поливектор — (от Поли... и Вектор         (математический), тензор, кососимметрический относительно любых двух своих индексов (см. Тензорное исчисление). Т. о., П. есть тензор, имеющий индексы либо только ковариантные (нижние), либо только контравариантные… …   Большая советская энциклопедия

  • КРУЧЕНИЕ — 1) К. к р и в о й величина, характеризующая отклонение пространственной кривой от соприкасающейся плоскости. Пусть Р произвольная точка кривой и Q точка кривой близкая Р, угол между соприкасающимися плоскостями кривой в точках Ри Q, а длина… …   Математическая энциклопедия

  • ПОЛИВЕКТОР — р вектор, векторного пространства V элемент р й внешней степени LPV пространства Vнад полем k(см. Внешняя алгебра). p вектор может пониматься как кососимметризованный рраз контравариантный тензор на V. Любая линейно независимая система векторов х …   Математическая энциклопедия

  • ТРИВЕКТОР — упорядоченная совокупность [ и, v, w]трех векторов и, v, w аффинного пространства А, отложенных от общего начала. Т. полагается равным нулю, если определяющие его векторы компланарны (линейно зависимы). Ненулевой Т. определяет несущую его 3… …   Математическая энциклопедия

  • Пфаффиан — Пфаффианом кососимметричной матрицы называется некоторый многочлен от её элементов, квадрат которого равен определителю этой матрицы. Как и определитель, пфаффиан является ненулевым только для матриц размера , и в этом случае его степень равна n …   Википедия

  • Векторное произведение — в трёхмерном пространстве. Векторное произведение  это псевдовектор, перпендикулярный плоскости, построенной по двум …   Википедия

  • Поливектор — Поливектор, р вектор, векторного пространства   элемент некоторой внешней степени пространства над полем . p вектор может пониматься как кососимметризованный р раз контравариантный тензор на . 2 вектор также называют бивектором, а 3 вектор… …   Википедия

  • Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»