ПУАССОНА ИНТЕГРАЛ

- интегральное представление решения Дирихле задачи для Лапласа уравнения в простейших областях. Так, П. и. для шара B_n (0, R).евклидова пространства , радиуса Rс центром в начале координат имеет вид

(1)

где f(у) - данная непрерывная функция на сфере S_n(0, R).радиуса R,

- ядро Пуассона для шара, s_n= =np^n/2R^n-1/Г(n/2+1) площадь сферы S_n(0, R), dS_n - элемент площади S_n(0, R).

С. Пуассон [1] пришел к формуле (1) в случае n=2 как к интегральной форме записи суммы тригонометрии, ряда

где a_k, b_k - коэффициенты Фурье функции f(y)=f(e^lj),(r,q) и (1, j)- полярные координаты соответственно точек х=rе ^iq и y= е ^iq, когда ядро Пуассона имеет вид

(2)

(о применениях П. и. в теории тригонометрич. рядов см. [3], а также Абеля - Пуассона метод суммирования).

П. и. для полупространства

имеет вид

(3)

где

- элемент площади , f (у) - ограниченная непрерывная функция на ,

- ядро Пуассона для полупространства. Формулы (1) и (3) суть частные случаи формулы Грина

(4)

дающей решение задачи Дирихле для областей с гладкой границей Г при помощи производной dG(x, y)/dn_y функции Грина G(x, у )по направлению внутренней нормали к Г в точке 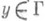. Иногда формулу (4) также наз. П. и.

Основные свойства П. и.: 1) и(х).есть гармонич. функция координат точки х;2) П. и. дает решение задачи Дирихле с граничными данными f(у).в классе (ограниченных) гармонич. функций, т. е. функция и(х), продолженная на границу области значениями f(y), непрерывна в замкнутой области. На этих свойствах основаны применения П. и. в классической математич. физике (см. [4]).

П. и., понимаемый в смысле Лебега, от суммируемой функции f(y), напр, на S_n(0, R), наз. интегралом Пуассона - Лебега; интеграл вида

(5)

по произвольной конечной борелевской мере m, сосредоточенной на S_n(0, R), наз. интегралом Пуассона - Стилтьеса. Класс Агармонич. функций и(х), представимых интегралом (5), характеризуется тем, что любая функция есть разность двух неотрицательных гармонич. функций в В _п(0, R). Класс функций, представимых интегралом Пуассона - Лебега, есть правильный подкласс класса А, содержащий, в свою очередь, все ограниченные гармонич. функции в В _п(0, R). Для почти всех точек по мере Лебега на S_n(0, R) интеграл Пуассона - Стилтьеса (5) имеет угловые граничные значения, совпадающие со значением производной m'(у). меры m по мере Лебега. Теория интегралов Пуассона - Стилтьеса и Пуассона - Лебега строится и для случая полупространства (см. [5]).

Большую роль в теории аналитич. ций многих комплексных переменных и в ее применениях к квантовой теории поля играют различные модификации П. и. Напр., ядро Пуассона для поликруга

комплексного пространства С ⁿ получается при перемножении ядер (2):

Соответствующий П. и.

по остову поликруга , j=1, . . ., n} дает кратногармонич. функцию , принимающую на остове Т ⁿ непрерывные значения f(z). Рассматриваются также обобщения в виде интегралов Пуассона - Лебега и Пуассона - Стилтьеса (см. [6]).

В квантовой теории поля применяются П. и. для трубчатых областей T^C комплексного пространства над выпуклым открытым острым конусом Св пространстве (с вершиной в начале координат) вида

П. и. для полуплоскости вида (3) при n=2 есть частный случай таких П. и. для трубчатых областей. П. и. для ограниченных симметрич. областей пространства С ⁿ представляется так же, как П. и. для трубчатой области в пространстве матриц. Понимая плотность П. и. f как обобщенную функцию, а сам П. и.- как свертку f с ядром Пуассона, приходят к важному понятию П. и. от обобщенных функций определенных классов (см. [7]-[9]).

Лит.:[1] Poiseon S. D., "J. Ecole polytechn.", 1820, t. 11, p. 295-341; 1823, t. 12, p. 404-509; [2] Schwarz H. A., "Vterteljahrsechr. Naturforsch. Oes. Zurich", 1870, Bd 15, 8. 113 - 28; [3] Бари Н. К., Тригонометрические ряды, М., 1961; [4] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 5 изд., М., 1977; [5] Соломенцев Е. Д., Итоги науки. Математический анализ. Теория вероятностей. Регулирование. 1962, М., 1984, с. 83-100; [6] Рудин У., Теория функций в поликруге, пер. с англ., М., 1974; [7] Владимиров В. С., Обобщенные функции в математической физике, М., 1976; [8] Хуа Ло - кен, Гармонический анализ функций многих комплексных переменных в классических областях, пер. с кит., М., 1959; [9] Стейн И., Вейс Г., Введение в гармонический анализ на евклидовых пространствах, пер. с англ., М., 1974. Е. Д. Соломенцев.