- ОСВЕЩЕНИЯ ЗАДАЧА
- задача определения минимального числа направлений пучков параллельных лучей или числа источников, освещающих всю границу выпуклого тела. Пусть К - выпуклое тело n-мерного линейного пространства
, a bd Ки int К - соответственно граница и внутренность его, причем 
. Наиболее известны следующие О. з.
1) Пусть l - нек-рое направление в пространстве Rn. Точка
наз. освещенной извне направлением l, если прямая, проходящая через х параллельно I, проходит через нек-рую точку 
и направление вектора 
совпадает с l. Ищется минимальное число с(К).направлений в пространстве 
, достаточное для освещения в атом смысле всего множества bd K.
2) Пусть z - нек-рая точка множества
Точка 
Кназ. освещенной извне точкой zесли прямая, определяемая точками z и х, проходит через нек-рую точку 
и векторы 
и 
одинаково направлены. Ищется минимальное число с' (К).точек из 
, достаточное для освещения в этом смысле всего множества bd К.
3) Пусть z - нек-рая точка множества bd К. Точка
наз. освещенной изнутри точкой 
, если прямая, определяемая точками z и х, проходит через нек-рую точку 
и векторы 
и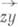 
противоположно направлены. Ищется минимальное число р(К).точек из bd K, достаточное для освещения изнутри всего множества bd К.
4) Система точек
наз. фиксированной для К, если она обладает свойствами: a) Zдостаточна для освещения изнутри всего множества bd K; б) Zне обладает никаким собственным подмножеством, достаточным для освещения изнутри множества bd K. Ищется максимальное число р' (К).точек фиксированной системы для тела 
.
Задача 1) была поставлена в связи с Хадвигера гипотезой (см. [1]): минимальное число тел b(К), гомотетичных ограниченному Кс коэффициентом гомотетии k,0<k<1, достаточное для покрытия К, удовлетворяет неравенству
, причем значение b(К)=2n характеризует параллелепипед. Для ограниченного 
. Если Кнеограниченно, то 
и существуют такие тела, что с(К)<b (К).или 
(см. [1]).
Задача 2) поставлена в связи с задачей 1). Для ограниченного
верно равенство с(К)=с' (К). Если же Кнеограниченно, то 
и 
. Число с' (К)для любого неограниченного
принимает одно из значений: 
(см. [1]).
Решение задачи 3) имеет вид: число р(К).определено тогда и только тогда, когда Котлично от конуса. В этом случае
,
причем р (K)=n+1 характеризует n-мерный симплекс пространства
(см. [1]).
Для задачи 4) (см. [2]) предполагается, что при ограниченном
верно неравенство
Каждая из О. з. тесно связана с нек-рым специальным покрытием тела К(см. [1]).
Лит.:[1] Болтянский В. Г., Солтан Н. С., Комбинаторная геометрия различных классов выпуклых множеств, Киш., 1978; [2] GriinbaumB., "Acta main. Acad. scihung.", 1964, v. 15, p. 161-63. П. С. Солтан.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
