ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ

-отображение векторного пространства в себя, при к-ром образом суммы двух векторов является сумма их образов, а образом произведения вектора на число - произведение образа вектора на это число. Если V - векторное пространство, f - заданное в нем Л. п. и ж, у - любые векторы пространства, 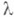- любое число (элемент поля), то

Если векторное пространство Vимеет конечную размерность - его базис; x₁, ,x₂, ..., х _п - координаты произвольного вектора жв этом базисе и у ₁, у ₂, . . ., у _п- координаты его образа то координаты вектора y выражаются через координаты. вектора як линейными однородными функциями

Матрица

наз. матрицей Л. п. f в базисе В ее столбцах стоят координаты образов базисных векторов. Если

- матрица перехода от базиса к базису

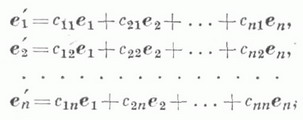
то в базисе матрица ВЛ. п. fбудет B= С ^-1 АС.

Суммой двух Л. п. f и gпаз. такое преобразование А, при к-ром для всякого вектора

Произведением Л. п. f на число l ваз. преобразование k, при к-ром для всякого вектора

Произведением Л. п. f на Л. п. gназ. преобразование

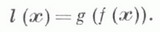
Сумма двух Л. п., произведение Л. п. на число, произведение двух Л. п. являются линейными преобразованиями. Л. п. образуют алгебру. В случае, когда конечномерное пространство имеет размерность п, алгебра его Л. п. изоморфна алгебре квадратных матриц порядка п, элементами к-рых являются элементы того поля, над к-рым построено векторное пространство.

Л. п. f, при к-ром векторное пространство отображается на себя, наз. обратимым, если существует такое преобразование f^-1, что

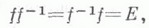
где Е - тождественное преобразование. Преобразование f^-1 является Л. п. и наз. обратным преобразованием к преобразованию f. Л. п., заданное в конечномерном векторном пространстве, обратимо тогда и только тогда, когда определитель его матрицы в каком-нибудь (и тогда во всяком) базисе отличен от нуля. Если А - матрица обратимого Л. п., то матрица обратного ему Л. п. f^-1 равна А ^-1. Обратимые Л. п. образуют группу по отношению к операции умножения. В случае векторных пространств конечной размерности и эта группа изоморфна группе невырожденных квадратных матриц порядка п.

Подпространство Vвекторного пространства Vназ. инвариантным подпространством относительно Л. п. f, если . для всякого вектора Ненулевой вектор наз. собственным вектором Л. п. f, соответствующим собственному значению если В случае пространства конечной размерности над полем комплексных чисел всякое Л. п. имеет собственный вектор (обладает одномерным инвариантным подпространством). В случае конечномерного пространства над полем действительных чисел у всякого Л. п. имеется одномерное или двумерное инвариантное подпространство. Л. п. f, заданное в конечномерном векторном пространстве, наз. диагонализируемым Л. п.,
если в пространстве Vсуществует такой базис, в к-ром матрица этого преобразования имеет диагональную форму. Другими словами, Л. п. диагонализируемо, еcли пространство обладает базисом, состоящим из собственных векторов этого Л. п. Однако не всякое Л. п. даже в пространстве над полем комплексных чисел обладает базисом из собственных векторов этого Л. п., напр. Л. п. двумерного пространства, заданное матрицей

у к-рой имеется единственное одномерное инвариантное подпространство с базисом {1, 0}.

В конечномерном векторном пространстве над полем комплексных чисел для всякого Л. п. существует такой базис, в к-ром матрица этого преобразования имеет клеточный вид, где по главной диагонали стоят жордановы клетки, а в остальных местах - нули. Жорданова клетка 1-го порядка состоит из одного числа К;жорданова клетка порядка kесть квадратная матрица порядка kвида

Числа l являются собственными значениями матрицы Л. п. Одному и тому же Я могут соответствовать как несколько клеток одного и того же порядка, так и клетки различных порядков. Матрица, состоящая из жордановых клеток, наз. нормальной жордановой формой матрицы.

Л. п. f, заданное в евклидовом (унитарном) пространстве, наз. самосопряженным (соответственно эрмитовым), если для всяких двух векторов имеет место равенство ) (соответственно

Л. п., заданное в конечномерном евклидовом (унитарном) пространстве, будет самосопряженным (эрмитовым) тогда и только тогда, когда его матрица Ав каком-нибудь (а тогда и во всяком) ортонормированном базисе является симметрической (соответственно эрмитовой). Самосопряженное (эрмитово) Л. п., заданное в конечномерном евклидовом (соответственно унитарном) пространстве, обладает ортонормированным базисом, в к-ром его матрица имеет диагональную форму. По главной диагонали стоят (всегда действительные) собственные значения матрицы АЛ. п.

Л. п. f, заданное в евклидовом (унитарном) пространстве V, наз. изометрическим (соответственно унитарным), если для всякого вектора

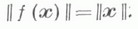
Л. п., заданное в конечномерном евклидовом (унитарном) пространстве, изометрично (соответственно унитарно) тогда и только тогда, когда его матрица Ав каком-нибудь (а тогда и во всяком) ортонормированном базисе была ортогональной (соответственно унитарной). Для всякого изометрич. Л. п., заданного в конечномерном евклидовом пространстве, существует ортонормированный базис, в к-ром матрица преобразования состоит из клеток 1-го и 2-го порядка, стоящих на ее главной диагонали. Клетки 1-го порядка суть действительные собственные значения матрицы Апреобразования, равные +1 и -1, а клетки 2-го порядка имеют вид

где - действительная часть и коэффициент при i комплексного собственного значения, матрицы А, на остальных местах матрицы Астоят нули. Для всякого унитарного преобразования, заданного в унитарном пространстве, существует ортонормированный базис, в к-ром матрица этого преобразования является диагональной, причем на главной диагонали стоят числа, по модулю равные 1.

Всякое Л. п., заданное в конечномерном евклидовом (унитарном) пространстве, является произведением самосопряженного и изометрич. Л. п. (соответственно эрмитова и унитарного).

Лит.:[1] Александров П. С., Лекции по аналитической геометрии..., М., 1968; [2] Гельфанд II. М., Лекции по линейной алгебре, 4 изд., М., 1971; [3] Ефимов Н. В., Розендорн 3. Р., Линейная алгебра и многомерная геометрия, М., 1970; [4] X а л м о ш П., Конечномерные векторные пространства, пер. с англ., М., 1963. А. С. Пархоменко.