ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ

ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ

- система дифференциальных уравнений

где

- почти

периодические отображения; в координатной записи:

тде - почти периодич. числовые функции. Такие системы возникли в связи с появлением Бора почти периодических функций (см. [1]). Интерес к более узкому классу систем (A(t).и f(t) - квазипериодич. отображения) появился значительно раньше в связи с рассмотрением уравнений в вариациях вдоль условно периодич. решений уравнений небесной механики. Если однородная система

есть система с интегральной разделенностью (см. Интегральной разделенности условие), то она почти периодическим по t Ляпунова преобразованием x=L(t)yприводится к диагональной системе y = B(t)yс почти периодич. коэффициентами, т. е. к такой, что существует не зависящий от tбазис в состоящий из векторов, являющихся при каждом собственными

векторами оператора В(t);в координатах по этому базису система y=B(t)yзаписывается в диагональном виде:

Множество систем с интегральной разделенностью открыто в пространстве систем (2) с почти периодич. коэффициентами, наделенном метрикой

Имеет место следующая теорема. Пусть где причем собственные значения Свсе действительны и различны, - почти периодич. отображение Тогда найдется такое, что при всех e таких, что система (2) почти периодическим по tпреобразованием Ляпунова приводится к диагональной системе с почти периодич. коэффициентами.

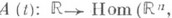
Для почти периодич. отображения следующие четыре утверждения эквивалентны друг другу: 1) для всякого почти периодич. отображения у системы (1) найдется почти периодич. решение; 2) имеет место экспоненциальная дихотомия решений системы (2); 3) ни одна из систем где не имеет ненулевых ограниченных решений; 4) для всякого ограниченного отображения 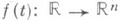у системы (1) найдется ограниченное решение.

Лит.:[1] Бор Г., Почти периодические функции, пер. с нем., М.- Л., 1934; [2] F a v а г 4 J., Lecons sur les fonctions prcsque periodiques, P., 1933; [3] Е р у г и н Н. П., Линейные системы обыкновенных дифференциальных уравнений с периодическими и квазипериодическими коэффициентами, Минск, 1963; [4] Массера X.-Л., Шеффер X.-X., Линейные дифференциальные уравнения и функциональные пространства, пер. с англ., М., 1970; [5] Мухамадиев Э., "Докл. АН СССР", 1971, т. 196, № 1, с. 47 - 49; [6] Итоги науки и техники. Математический анализ, т. 12, М., 1974, с. 71-146.

В. М. Миллионщиков.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Полезное


Смотреть что такое "ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ" в других словарях:

  • ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ — система плинейных дифференциальных уравнений вида где t действительная переменная, комплекснозначные функции, причем Число T>0 наз. периодом коэффициентов системы (1). Систему (1) удобно записывать в виде одного векторного уравнения где… …   Математическая энциклопедия

  • КАЧЕСТВЕННАЯ ТЕОРИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ — математическая дисциплина, изучающая свойства решений обыкновенных дифференциальных уравнений без нахождения самих решений. Основы К. т. д. у. были заложены в конце 19 в. А. Пуанкаре (см. [1], [2]) и А. М. Ляпуновым (см. [3], [4]). А. Пуанкаре… …   Математическая энциклопедия

  • ПОЧТИ ПРИВОДИМАЯ ЛИНЕЙНАЯ СИСТЕМА — обыкновенных дифференциальных уравнений система . (*) обладающая свойством: найдется система с постоянными коэффициентами , и для каждого в>0 найдется Ляпунова преобразование Lg(t). такие, что в результате замены x=Le(t)y система (*).переходит …   Математическая энциклопедия

  • ПРАВИЛЬНАЯ ЛИНЕЙНАЯ СИСТЕМА — обыкновенных дифференциальных уравнений система вида (1) (где суммируемое на каждом отрезке отображение , обладающая свойством: существует и равен , где Ляпунова, характеристические показатели системы (1). Для того чтобы треугольная система была… …   Математическая энциклопедия

  • ГАМИЛЬТОНОВА СИСТЕМА ЛИНЕЙНАЯ — система вида где Н квадратичная форма с действительными коэффициентами от переменных с коэффициентами, к рые могут зависеть от времени t. Г. с. л. наз. также линейной канонической системой. Система (1) может быть записана в векторной форме: где х …   Математическая энциклопедия

  • ОСОБЫЕ ПОКАЗАТЕЛИ — линейной системы обыкновенных дифференциальных уравнений величины, определяемые формулой: (верхний особый показатель) или формулой (нижний особый показатель), где Коши оператор системы где отображение , суммируемое на каждом отрезке. О. п. могут… …   Математическая энциклопедия

  • УСТОЙЧИВОСТЬ ХАРАКТЕРИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ — свойство Ляпунова характеристических показателей линейной системы обыкновенных дифференциальных уравнений где непрерывное отображение (или удовлетворяющее условию Говорят, что характеристич. показатели Ляпунова системы (1) устойчивы, если каждая… …   Математическая энциклопедия

  • ЦЕНТРАЛЬНЫЕ ПОКАЗАТЕЛИ — линейной системы обыкновенных дифференциальных уравнений величины, определяемые формулами (верхний центральный показатель) и (нижний центральный показатель); иногда нижним Ц. п. называется величина Здесь Коши оператор системы где суммируемое на… …   Математическая энциклопедия

  • УСТОЙЧИВОСТИ ТЕОРИЯ — совокупность взгля дов, представлений, идей, понятий, рассуждении, методов, теорий (содержащих определения, леммы, теоремы и доказательства), возникших и возникающих с целью изучения устойчивости движения (понимаемого в самом общем виде). Таким… …   Математическая энциклопедия

  • СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ; — численные методы нахождения методы вычисления собственных значений и соответствующих собственных функций дифференциальных операторов. Колебания упругих ограниченных тел описываются уравнением где нек рое дифференциальное выражение. Если решение… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»