Сопряжённое априорное распределение — (англ. conjugate prior) и сопряжённое семейство распределений одни из основных понятий в байесовской статистике. Рассмотрим задачу о нахождении распределения параметра (рассматриваемого как случайная величина) по имеющемуся наблюдению . По… … Википедия
Некорректное априорное распределение — ситуация, когда в теореме Байеса сумма (интеграл) априорных вероятностей не даёт в результате 1 или вообще не ограничена. Обоснование Если теорему Байеса записать следующим образом: то становится ясным, что она останется верной если все априорные … Википедия
Распределение Дирихле — В теории вероятностей и математической статистике распределение Дирихле (по имени Иогaнна Пeтера Гyстава Лежён Дирихлe) часто обозначаемое Dir(α) это семейство непрерывных многомерных вероятностных распределений параметризованных вектором α… … Википедия
НАИМЕНЕЕ БЛАГОПРИЯТНОЕ РАСПРЕДЕЛЕНИЕ — априорное распределение, максимизирующее функцию риска в статистич. задаче принятия решения. Пусть по реализации случайной величины X, принимающей значения в выборочном пространстве ( , надлежит принять решение dиз пространства решений при этом… … Математическая энциклопедия
Априорная вероятность Джеффри — В байесовской статистике априорная вероятность Джеффри, по имени Гарольда Джеффри неинформативная (объективная) априорная вероятность в пространстве параметра, пропорциональная квадратному корню из детерминанта информации Фишера: Её ключевая… … Википедия
Априорная вероятность — В байесовском статистическом выводе априорное распределение вероятностей (англ. prior probability distribution, или просто prior) неопределённой величины p распределение вероятностей, которое выражает предположения о p до учёта… … Википедия
Теорема о конце света — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Теорема о конце света (Doomsday argument, сокращённо далее DA, нет устоявшегося перевода на русский язык, обычно используют английское … Википедия
Света аргумент — Теорема о конце света (Doomsday argument, сокращённо далее DA, нет устоявшегося перевода на русский язык, обычно используют английское название или сокращение DA) это вероятностное рассуждение, которое претендует на то, чтобы предсказывать… … Википедия
Максимальная апостериорная гипотеза — В статистике метод оценки Максимальной апостериорной гипотезы (MAP) тесно связан с методом максимального правдоподобия (ML), но использует дополнительную оптимизацию, которая совмещает априорное распределение величины, которую хочет оценить.… … Википедия
Оценка апостериорного максимума — В статистике метод оценки с помощью апостериорного максимума (MAP) тесно связан с методом максимального правдоподобия (ML), но дополнительно при оптимизации использует априорное распределение величины, которую оценивает. Содержание 1 Введение 2… … Википедия
- пара случайных величин (случайных векторов или более общих случайных элементов). Случайную величину 
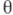рассматривают как неизвестный параметр, а X - как результат наблюдений, предназначенных для оценки 
. Совместное распределение 
задают распределением 
(которое п называют в этом случае А. р.) и совокупностью условных распределений 
случайной величины 
по отношению к 
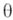. По Бейеса формуле можно вычислить условное распределение 
относительно X(которое в этом случае называют апостериорным распределением 
). В статистпч. задачах часто А. р. неизвестно (и даже само предположение о его существовании не представляется достаточно обоснованным). Об использовании А. р. см. Бейесовский подход.