КВАДРИКА

- 1) К.- поверхность 2-го порядка. В трехмерном пространстве (проективном, аффинном или евклидовом) К. есть множество точек, однородные координаты х ₀, х ₁, х ₂, х ₃ к-рых (относительно проективной, аффинной или декартовой системы координат) удовлетворяют однородному уравнению 2-й степени:

Билинейная симметричная форма

наз. полярной формой относительно F(x). Две точки М'( х'₀, х'₁, х'₂, х'₃), М"( х"₀, х"₁, х"₂, х"₃), для которых Ф ( х', х") =0, наз. полярно сопряженными точками относительно К. Если прямая ( М', М" )пересекает К. в точках N₁, N₂ и точки М', М" полярно сопряжены относительно К., то точки N₁, N₂ и М', М" образуют гармоническую четверку. Точки К. и только они являются самосопряженными. Прямая, каждая точка к-рой принадлежит К., наз. прямолинейной образующей К. Полюсом данной плоскости относительно К. наз. точка, полярно сопряженная со всеми точками этой плоскости. Множество точек пространства, полярно сопряженных с данной точкой М' относительно К., наз. полярой точки М' относительно К. Касательная плоскость к К.- поляра точки касания. Поляра точки М' определяется линейным уравнением Ф ( х, х') =0относительно координат х ₀, х ₁, х ₂, х ₃. Если то поляра точки М'- плоскость; если то поляра точки М'- все пространство. В этом случае точка М' принадлежит К. и наз. ее особой точкой. Если число R = rang(a_ij) = 4, то К. не имеет особых точек и наз. невырождающейся К. В проективном пространстве это - мнимый овалоид, действительный овалоид или линейчатая К. Невырождающаяся К. определяет корреляцию - биективное отображение множества точек проективного пространства на множество плоскостей. Линейчатая невырождающаяся К. имеет два различных семейства прямолинейных образующих, расположенных на К. так, что всякие две прямые одного семейства не пересекаются, а две прямые разных семейств пересекаются в одной точке. Если R=3, то К. является конусом (действительным или мнимым) с вершиной в единственной особой точке. Действительный конус имеет единственное семейство прямолинейных образующих, проходящих через его вершину. Если R=2, то К. распадается на пару плоскостей (действительных или мнимых), пересекающихся по прямой, состоящей из особых точек. Если R=1, то К. является сдвоенной действительной плоскостью, образованной особыми точками К. Аффинные свойства К. выделяются спецификой расположения К., ассоциированных с ней точек, прямых и плоскостей относительно выделенной плоскости x₀=0 - несобственной плоскости. Напр., эллипсоид (гиперболоид, параболоид) - невырожденная К., не пересекающая (пересекающая, касающаяся) несобственную плоскость. Центр К.- полюс несобственной плоскости; диаметр - прямая, полярно сопряженная несобственной прямой.

Лит.:[1] Фиников С. П., Аналитическая геометрия, 2 изд., М., 1952; [2] Ефимов Н. В., Краткий курс аналитической геометрии, 5 изд., М., 1960.

В. С. Малаховский.

2) К. в алгебраической геометрии - проективное алгебраическое многообразие, определяемое однородным квадратным уравнением

в проективном пространстве Р ^п над основным полем k. Пусть далее основное поле алгебраически замкнуто с характеристикой, не равной 2. Пусть Q- К. в Р ^п и s(Q)- множество ее особых точек. Тогда s(Q)- пустое множество, если и только если rk(Q)=n+l, где rk(Q)- ранг соответствующей квадратичной формы. Если s{Q )не пусто, то Q- конус над гладкой К. размерности rk(Q)-1, вершиной к-рого является проективное подпространство s(Q)в Р ^п размерности п-rk(Q). Все К. с rk(Q)=r проективно эквиваленты К.

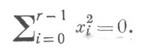
Пусть s (Q)пусто и - линейное подпространство максимальной размерности (оно наз. образующей квадрики Q), тогда

а) если dim Q=2m, то dim E=m;

б) если dim Q=2m+1, то dim E=m.

Кроме того, семейство всех подпространств Емаксимальной размерности на Qявляется замкнутым неособым подмножеством Gграссманова многообразия подпространств размерности dim Eв Р ^п, причем, если dim Q-2m, то G_i, i=i,2,- непересекающиеся неособые неприводимые рациональные многообразия одинаковой размерности (₂^m+1), a Eи Е' принадлежат одной и той же компоненте, если и только если

Если же dim Q=2m+l, то Gявляется неособым и неприводимым рациональным многообразием размерности (₂^m+2)-

В случае, когда s(Q)пусто и dim Q=2, если же то

Любая К. рациональна: бирациональный изоморфизм К. Qс проективным пространством задается стереографич. проекцией К. Qиз нек-рой точки

Многообразия, являющиеся полными пересечениями К., изучаются с точки зрения бирациональной геометрии [3]. Пересечения двух К. изучены в [2], трех - в [4].

Любое проективное многообразие Xможет быть так погружено в проективное пространство P^N (для достаточно большого N), что его образ является пересечением (как правило, неполным) К., его содержащих [1].

Изучение К. над незамкнутыми полями тесно связано с арифметикой квадратичных форм.

Лит.:[1] Mumlord D., С. I. M. E. III ciclo. Varenna, 1969, Roma, 1970, p. 29-100; [2] Reid M., The complete intersection of two or more quadrics, These D. Ph. Cambridge Univ., 1972; [3] Roth L., Algebraic threefols (with special regard to problems of rationality), B.-Hdlb.-N.Y., 1955; [4] Тюрин А. Н., "Успехи матем. наук", 1975, т. 30, № 6, с. 51-99.

В. А. Искоеских.