ИЗОЛИРОВАННАЯ ОСОБАЯ ТОЧКА

для элемента аналитической функции f(z)- точка акомплексной плоскости z, относительно к-рой выполняются условия: 1) этот элемент функции f(z)не допускает аналитического продолжения по какому-либо пути в точку я; 2) существует такое число R>0, что в проколотой окрестности U= {: 0<|z- а|<R} точки ааналитич. продолжение элемента f(z) возможно по любому пути.

Если при аналитич. родолжении f(z) вдоль замкнутого пути, расположенного в Uи окружающего а, напр, вдоль окружности |z-a|=p,0<r<D, получается новый элемент, отличный от исходного, то аназ. ветвления точкой, или И. о. т. многозначного характера. В противном случае элемент f(z)определяет однозначную аналитич. функцию в Uи аназ. И. о. т. однозначного характера. В проколотой окрестности UИ. о. т. а однозначного характера функция f(z) разлагается в Лорана ряд:

с правильной частью f₁(z)=и главной частью f₂(z)= Поведение аналитич. функции f(z). в проколотой окрестности UИ.o. т. однозначного характера определяется в основном главной частью ряда Лорана. Если все коэффициенты главной части равны нулю, то, полагая f(a)=c₀, получим однозначную аналитич. функцию в полной окрестности а. Этот случай фактического отсутствия особенности характеризуется также тем, что f(z)ограничена в проколотой окрестности U, или тем, что существует конечный предел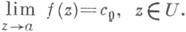

Если среди коэффициентов главной части имеется лишь конечное число отличных от нуля и наименьший номер среди них имеет с_ _т неравно 0, то аесть полюс порядка т. Полюс ахарактеризуется также тем, что

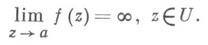
Наконец, если среди коэффициентов главной части имеется бесконечное множество отличных от нуля, то а- существенно особая точка. В этом случае не существует конечного или бесконечного предела

Для бесконечно удаленной И. о. т. элемента f{z )проколотая окрестность имеет вид U={'. r<|z| <}, а ряд Лорана -

Здесь правильная часть а главная часть С этими условиями описанные выше классификация и признаки типов И. о. т. без дальнейших изменений переносятся на случай а= бесконечность (см. также Вычет). Следует отметить, что элементы различных ветвей полной аналитической функции f(z) в одной и той же точке могут иметь особенности совершенно различных типов.

Голоморфные функции f(z)многих комплексных переменных, z= (z_l, z₂, . . ., z_n), при не могут иметь И. о. т. При особые точки составляют бесконечные множества особенностей.

Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., М., 1976.

Е. Д. Соломенцев.