ДИРИХЛЕ РЯД

- функциональный ряд вида

где а _п -комплексные коэффициенты; l _п, 0< -показатели Д. p., s= s+ it - комплексное переменное. При l_n=ln пполучается так наз. обыкновенный ряд Дирихле

Ряд

представляет для s>1 дзета-функцию Римана. Ряды

где х(п)- функция, наз. Дирихле характером, изучались П. Дирихле (см. Дирихле L-функция). Ряды (1) с произвольными показателями l _п наз. общими рядами Дирихле.

Общие ряды Дирихле с положительными показателями. Пусть сначала l _п- положительные числа. Имеет место аналог Абеля теоремы для степенных рядов: если ряд (1) сходится в точке s₀=s₀+it₀, то он сходится в полуплоскости s>s₀, причем внутри любого угла |arg(s-s₀)| <j₀<p/2 сходится равномерно. Открытая область сходимости ряда есть нек-рая полуплоскость s>с. Число с наз. абсциссой сходимости Д. р., прямая s= с- прямой сходимости Д. р., полуплоскость s>с - полуплоскостью сходимости Д. р. Наряду с полуплоскостью сходимости рассматривается полуплоскость абсолютной сходимости Д. р.: s>а - открытая область, в к-рой ряд сходится абсолютно (при этом а- абсцисса абсолютной сходимости). Абсциссы сходимости и абсолютной сходимости, вообще говоря, различны; всегда

причем имеются Д. р., для к-рых а-c=d. В случав d=0 для вычисления абсциссы сходимости (абсциссы абсолютной сходимости) имеется формула

представляющая собой аналог формулы Коши - Адамара. Случай d>0 сложнее: если величина

положительна, то с=b; если и ряд (1) в точке s=0 расходится, то с=0; если и ряд (1) в точке s=0 сходится, то

Сумма ряда F(s)в полуплоскости сходимости есть аналитич. функция. При функция F(s). ведет себя асимптотически как первый член ряда: а ₁ е ^-l1s (если а неравно 0). Если сумма ряда равна нулю, то и все коэффициенты ряда равны нулю. Максимальная полуплоскость s>h, в к-рой F(s)является аналитич. функцией, наз. полуплоскостью голоморфности функции F(s), прямая s =h наз. прямой голоморфности. Справедливо неравенство h<с, причем возможны случаи, когда h<с. Пусть q- нижняя грань таких чисел b, что в полуплоскости s>b функция F(s)по модулю ограничена (q<а). Имеет место формула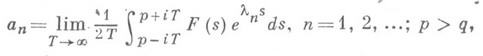

из к-рой вытекают неравенства

представляющие собой аналог неравенств Коши для коэффициентов степенного ряда.

Сумма Д. р. не может быть произвольной функцией, аналитической в какой-либо полуплоскости s>h: она, напр., должна стремиться к нулю при Однако имеет место следующий факт: какова бы ни была функция j(s), аналитическая в полуплоскости s>h, найдется такой Д. р. (1), что его сумма F(s)будет отличаться от j(s) на целую функцию.

Если последовательность показателей имеет плотность 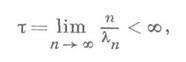то разность между абсциссой сходимости (абсциссы сходимости и абсолютной сходимости совпадают) и абсциссой голоморфности не превосходит величины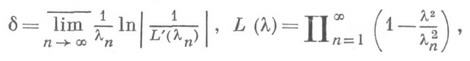

причем имеются ряды, для к-рых эта разность равна 6. Величина d может быть любой из в частности, если n=1, 2, . . ., то d=0. Прямая голоморфности обладает тем свойством, что на ней в любом отрезке длины 2pt у суммы ряда имеется хотя бы одна особенность.

Если Д. р. (1) сходится во всей плоскости, то его сумма F(s)есть целая функция. Пусть

R- порядком целой функции F(s) (порядком по Ритту) наз. величина

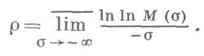
Через коэффициенты ряда она выражается по формуле

Можно также ввести понятие R-т ипа функции F(s). Если

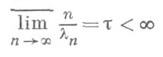
и если в горизонтальной полосе ширины, большей 2pt, функция F(s)по модулю ограничена, то F(s)=0 (аналог Лиувилля теоремы).

Ряды Дирихле с комплексными показателями. У Д. р.

(2)

с комплексными показателями открытая область абсолютной сходимости выпукла. Если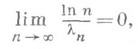

то открытые области сходимости и абсолютной сходимости совпадают. Сумма F(s)ряда (2) в области сходимости есть аналитич. функция. Область регулярности функции F(s), вообще говоря, шире области сходимости Д. р. (2). При условии

область регулярности выпукла. Пусть

L(X)- какая-нибудь целая функция экспоненциального типа, к-рая в точках l _п,имеет простые нули, y(t)- функция, ассоциированная по Борелю с L(X) (см. Бореля преобразование), D- наименьшее выпуклое замкнутое множество, содержащее все особенности функции y(t), и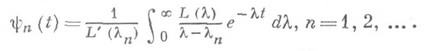

Тогда функции y_n(t) регулярны вне 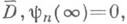и они обладают свойством биортогональности к системе {е^lns }:

где С- замкнутый контур, охватывающий В том случае, когда y_n(t) непрерывны вплоть до границы области 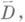в качестве Сможно взять границу дD. Произвольной функции F(s), аналитической в D(открытой части области ) и непрерывной в отнесем ряд

Для данной конечной выпуклой области 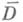можно построить такую целую функцию ИХ )с простыми нулями l₁, l₂, . .., что для любой функции F(s), аналитической в Dи непрерывной в ряд (3) равномерно сходится внутри Dи сходится к F(s). Для функции j(s), аналитической в D(не обязательно непрерывной в ), можно найти целую функцию нулевого экспоненциального типа

и функцию F(s), аналитическую в Dи непрерывную в такие, что

Тогда

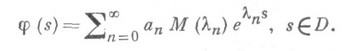
Представление произвольных аналитич. функций

Д. р. в области Dустановлено также в случаях, когда D- вся плоскость или D- выпуклая бесконечная многоугольная область (ограниченная конечным числом прямолинейных отрезков).

Лит.:[1] Леонтьев А. Ф., Ряды экспонент, М., 1976; [2] Мандельбройт С, Ряды Дирихле, принципы и методы, пер. с англ., М., 1973.

А. Ф. Леонтьев.