ДАНЖУА ИНТЕГРАЛ

ДАНЖУА ИНТЕГРАЛ

- 1) Данжуа узкий (специальный) интеграл - обобщение понятия интеграла Лебега. Функция f(x). наз. интегрируемой в смысле узкого (специального, D*) интеграла Данжуа на [ а, b], если существует такая непрерывная функция F(x)на [ а, b], что F'(x)=f(x)почти всюду, и каково бы ни было совершенное множество Р, существует порция Р, на к-рой F(x)абсолютно непрерывна и где 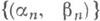- совокупность смежных интервалов к порции 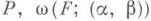- колебание на

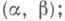
при этом

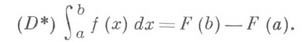
Такое обобщение интеграла Лебега ввел А. Данжуа [1]; он показал, что этот интеграл восстанавливает функцию по ее точной конечной производной. Интеграл D*' эквивалентен Перрона интегралу.

2) Данжуа широкий (общий) интеграл - обобщение понятия узкого Д. и. Функция f(x)наз. интегрируемой в смысле широкого (общего, D)интеграла Данжуа на [ а, b], если существует такая непрерывная функция F(x). на [а, b], что ее аппроксимативная производная почти всюду равна f(x)и каково бы ни было совершенное множество Р, существует порция Р, на к-рой F(x)абсолютно непрерывна; при этом

Введен независимо и почти одновременно А. Данжуа [2] и А. Я. Хинчиным [3], [4]. Интеграл Dвосстанавливает непрерывную функцию по ее точной конечной аппроксимативной производной.

3) Тотализация (T2S)0 представляет собой конструктивно определенный интеграл для решения задачи построения такого обобщения интеграла Лебега, к-рое позволило бы всякий всюду сходящийся тригонометрич. ряд рассматривать в качестве ряда Фурье (по этому интегралу). Введена А. Данжуа [5].

4) Тотализация (T2S )отличается от тотализации (T2S)0 тем, что при определении тотализации (T2S)0 обычный предел заменен на аппроксимативный. Для тотализации (T2S )А. Данжуа [5] дал и дескриптивное определение.

О взаимосвязях тотализации (T2S)0 и (T2S )с другими интегралами см. [6].

Лит.:[1] Denjoy А., "С. r. Acad. sci.", 1912, t. 154, p. 859-62, 1075-78; [2] его же, там же, 1916, t. 162, р. 377 -80; [3] Кhintсhine А., там же, 1916, t. 162, p. 287-91; [4] Xинчин А. Я., "Матем. сб.", 1918, т. 30, с. 543-57; [5] Denjоу A., Lecons sur le calcul des coefficients d'une serie trigonometrique, pt 1-4, P., 1941-49; [6] Виноградова И А, Скворцов В. А., в кн.: Итоги науки. Математический анализ. 1970, М., 1971, с. 65-107; [7] Сакс С, Теория интеграла, пер. с англ., М., 1949.

Т. <П. <Лукашенко


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "ДАНЖУА ИНТЕГРАЛ" в других словарях:

  • ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… …   Математическая энциклопедия

  • Интеграл Курцвейля — Интеграл Курцвейля  Хенстока  обобщение интеграла Римана, позволяет полностью решить задачу о восстановлении дифференцируемой функции по её производной. Ни интеграл Римана (в том числе и несобственный), ни интеграл Лебега не дают… …   Википедия

  • Интеграл Курцвейля-Хенстока — В математике, Интеграл Курцвейля Хенстока является обобщением интеграла Римана, позволяющим полностью решить задачу о восстановлении дифференцируемой функции по её производной. Ни интеграл Римана (в том числе и несобственный), ни интеграл Лебега… …   Википедия

  • Интеграл — (от лат. integer целый)         одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости… …   Большая советская энциклопедия

  • ХИНЧИНА ИНТЕГРАЛ — обобщение узкого Данжуа интеграла, введенное А. Я. Хинчиным [1]. Функция f(x)наз. интегрируемой в смысле Xинчина на [ а, b], если она интегрируема широким интегралом Данжуа и ее неопределенный интеграл почти всюду дифференцируем. Иногда интеграл… …   Математическая энциклопедия

  • БОКСА ИНТЕГРАЛ — одно из обобщений интеграла Лебега, предложенных А. Данжуа (A. Denjoy, 1919), подробно изученное Т. Дж. Боксом (Т. J. Boks, 1921). Действительная функция f(x).на отрезке [ а, Ь]периодически (с периодом b a) продолжается на всю прямую. Для… …   Математическая энциклопедия

  • ГАРНАКА ИНТЕГРАЛ — обобщение несобственного интеграла Римана на класс функций f, множество точек неограниченности к рых имеет нулевую жорданову меру и к рые интегрируемы по Риману во всяком сегменте, не содержащем точек из . Пусть конечная система интервалов,… …   Математическая энциклопедия

  • ПЕРРОНА ИНТЕГРАЛ — обобщение понятия интеграла Лебега. Функция f(x).наз. интегрируемой на [ а, b] в смысле Перрона, если существуют функции М(х).(мажоранта) и т(х). (миноранта) такие, что ( и нижняя и верхняя производные) для и нижняя грань значений М(b).мажорант… …   Математическая энциклопедия

  • МЕТРИЧЕСКАЯ ТЕОРИЯ ФУНКЦИЙ — раздел теории функций действительного переменного, в к ром свойства функций изучаются на основе понятия меры множества. Исследованиями многих математиков 19 в. была создана новая математич. дисциплина теория функций действительного переменного. К …   Математическая энциклопедия

  • ПЕРВООБРАЗНАЯ — (примитивная) функция, для конечной функции f(x) такая функция F(x), что всюду . Это определение является наиболее распространенным, но встречаются и другие, в к рых ослаблены требования существования всюду конечной F и выполнения всюду равенства …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»