Д'АЛАМБЕРА ФОРМУЛА

Д'АЛАМБЕРА ФОРМУЛА

- формула, выражающая решение задачи Коши для волнового уравнения с одной пространственной переменной. Пусть заданные функции j(х), y(х)принадлежат соответственно пространствам и 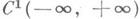, a f(t, х )непрерывна вместе с первой производной по хв полуплоскости Тогда классич. решение u(t, х )в Коши задачи

выражается Д. ф.:

Если функции j(х) и y(х) заданы и удовлетворяют указанным условиям гладкости на интервале , а - в треугольнике

то Д. ф. дает единственное решение задачи (1), (2) в QTx0.Требования на заданные функции могут быть ослаблены, если интересоваться решениями в нек-ром обобщенном смысле. Напр., из Д. ф. следует, что при f, интегрируемой по любому треугольнику , локально интегрируемой y и непрерывной ф можноопределить слабое решение задачи Коши (1),(2) как равномерный (в любом ) предел классич. решений (с гладкими данными) и оно также выражается Д. ф.

Формула названа по имени Ж. Д'Аламбера (J. D'Alembert, 1747).

Лит.:[1] Владимиров В. С, Уравнения математической физики, 2 изд., М., 1971; [2] Тихонова А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

А. К. Гущин.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "Д'АЛАМБЕРА ФОРМУЛА" в других словарях:

  • Формула Кирхгофа — Формула Кирхгофа  аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём трёхмерном пространстве. Методом спуска (то есть уменьшением размерности) из него можно… …   Википедия

  • Формула Д'Аламбера — Формула Кирхгофа  аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного… …   Википедия

  • Формула Д’Аламбера — Формула Кирхгофа  аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного… …   Википедия

  • Формула Пуассона — Формула Кирхгофа  аналитическое выражение для решения гиперболического уравнения в частных производных (т. н. «волнового уравнения») во всём пространстве. Методом спуска (то есть уменьшением размерности) из него можно получить решения двумерного… …   Википедия

  • ПУАССОНА ФОРМУЛА — 1) То же, что Пуассона интеграл.2) Формула, дающая интегральное представление решения задачи Коши для волнового уравнения в пространстве : и имеющая вид (1) где среднее значение функции j на сфере Sat в пространстве ( х, у, z) радиуса at с… …   Математическая энциклопедия

  • Принцип Д’Аламбера — Д’Аламбера принцип  в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится… …   Википедия

  • КИРХГОФА ФОРМУЛА — ф ла, выражающая регулярное решение и (х, t )неоднородного волнового уравнения в трёхмерном пространстве через нач. данные задачи Коши и (х,0)= ( х), ut (х,0) = = ( ас )и объёмный запаздывающий потенциал ( х, t) с плотностью f(y, t) …   Физическая энциклопедия

  • Д’Аламбер, Жан Лерон — Жан Лерон Д’Аламбер фр. Jean Le Rond D Alembert …   Википедия

  • Д'Аламбер — Латур. Жан Лерон Даламбер. Жан Лерон Д’Аламбер (д’Аламбер, Даламбер; фр. Jean Le Rond d Alembert, D Alembert; 16 ноября 1717  29 октября 1783)  французский учёный энциклопедист. Широко известен как философ, математик и механик. Член Парижской… …   Википедия

  • Д'Аламбер Жан Лерон — Латур. Жан Лерон Даламбер. Жан Лерон Д’Аламбер (д’Аламбер, Даламбер; фр. Jean Le Rond d Alembert, D Alembert; 16 ноября 1717  29 октября 1783)  французский учёный энциклопедист. Широко известен как философ, математик и механик. Член Парижской… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»