- ГОЛОНОМИИ ГРУППА
- одна из характеристик связности в расслоенном пространстве. Г. г. определяется для главного расслоенного многообразия Р со структурной группой Ли Gи базой В(обладающей счетным базисом), в к-ром задана инфинитезимальная связность Г. Одновременно она определяется для любого присоединенного к Ррасслоенного многообразия Е, слоями к-рого являются экземпляры нек-рого пространства Fпредставления группы Ли G.
Связность Г в Р (соответственно в Е).определяет для любой кусочно гладкой кривой Lбазы Визоморфное отображение ГLдруг на друга слоев, соответствующих началу и концу кривой L. Каждой кусочно гладкой замкнутой кривой Lбазы В, начинающейся и оканчивающейся в точке
 , соответствует автоморфизм слоя Gx (соответственно
, соответствует автоморфизм слоя Gx (соответственно  ) над точкой х. Множество этих автоморфизмов образует группу Ли
) над точкой х. Множество этих автоморфизмов образует группу Ли  , которая наз. группой голономии связности Г в точке х.
, которая наз. группой голономии связности Г в точке х.
Если база (линейно) связна, то
 и
и 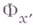 изоморфны между собой для любых
изоморфны между собой для любых 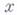 и
и  в В. Поэтому можно говорить о группе голономии Ф линейно связного многообразия Р(или Е).со связностью Г.
в В. Поэтому можно говорить о группе голономии Ф линейно связного многообразия Р(или Е).со связностью Г.
Г. г. Ф х является подгруппой структурной группы G. В случае линейной связности в Рэту подгруппу можно определить непосредственно. Пусть задана точка
 в слое
в слое  над точкой х. Совокупность элементов
над точкой х. Совокупность элементов  таких, что точки
таких, что точки  соединимы горизонтальными кривыми в Р, образует подгруппу
соединимы горизонтальными кривыми в Р, образует подгруппу  группы G, изоморфную
группы G, изоморфную  .
.
Ограниченной (суженной) Г. г.
 наз. подгруппа Г. г.
наз. подгруппа Г. г.  , порожденная замкнутыми кривыми, гомотопными нулю. Она совпадает с линейно связной компонентой единичного элемента Г. г.
, порожденная замкнутыми кривыми, гомотопными нулю. Она совпадает с линейно связной компонентой единичного элемента Г. г.  , при этом
, при этом 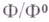 не более чем счетно.
не более чем счетно.
Роль Г. г. в дифференциальной геометрии расслоенных пространств выясняют следующие теоремы о линейных связностях в Р.
Теорема о приведении связности. Пусть
 - главное расслоенное пространство, удовлетворяющее второй аксиоме счеткости; Ф - Г. г. заданной в Рсвязности Г. Тогда структурная группа Gприводима к своей подгруппе Ф, а связность Г приводима к связности в приведенном расслоении
- главное расслоенное пространство, удовлетворяющее второй аксиоме счеткости; Ф - Г. г. заданной в Рсвязности Г. Тогда структурная группа Gприводима к своей подгруппе Ф, а связность Г приводима к связности в приведенном расслоении  , Г. г. к-рого совпадает с Ф.
, Г. г. к-рого совпадает с Ф.
Теорема о голономии. Алгебра голономии (алгебра ограниченной Г. г.) является подалгеброй алгебры G, порожденной всеми векторами
 , где
, где  - форма кривизны в точке у, у прооегает множество, каждая точка к-рого может быть соединена с исходной точкой y0 горизонтальным путем,
- форма кривизны в точке у, у прооегает множество, каждая точка к-рого может быть соединена с исходной точкой y0 горизонтальным путем,  - произвольные горизонтальные векторы.
- произвольные горизонтальные векторы.
Лит.:[1] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Бишоп Р. Л., Криттенден Р. Геометрия многообразий, пер. с англ., М., 1967; [3] Стернбсрг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970.
Г. Ф. Лаптев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
