Зоны Френеля

        участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (См. Дифракция света) (или звука). Впервые этот метод применил О. Френель в 1815—19. Суть метода такова. Пусть от светящейся точки Q (рис.) распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке Р. Разделим поверхность волны S на кольцевые зоны; для этого проведём из точки Р сферы радиусами PO, Pa = PO + ^λ/₂; Pb = Pa + ^λ/₂, Pc = Pb + ^λ/₂, (О — точка пересечения поверхности волны с линией PQ; λ — длина световой волны). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется З. Ф. Волновой процесс в точке Р можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой З. Ф. в отдельности. Амплитуда таких колебаний медленно убывает с возрастанием номера зоны (отсчитываемого от точки О), а фазы колебаний, вызываемых в Р смежными зонами, противоположны. Поэтому волны, приходящие в Р от двух смежных зон, гасят друг друга, а действие зон, следующих через одну, складывается. Если волна распространяется, не встречая препятствий, то, как показывает расчёт, её действие (сумма воздействий всех З. Ф.) эквивалентно действию половины первой зоны. Если же при помощи экрана с прозрачными концентрическими участками выделить части волны, соответствующие, например, N нечётным зонам Френеля, то действие всех выделенных зон сложится и амплитуда колебаний U_нечёт в точке Р возрастёт в 2N раз, а интенсивность света в 4N² раз, причём освещённость в точках, окружающих Р, уменьшится. То же получится при выделении только чётных зон, но фаза суммарной волны U_чёт будет иметь противоположный знак.

         Такие зонные экраны (т. н. линзы Френеля) находят применение не только в оптике, но и в акустике и радиотехнике — в области достаточно малых длин волн, когда размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).

         Метод З. Ф. позволяет быстро и наглядно составлять качественное, а иногда и довольно точное количественное представление о результате дифракции волн при различных сложных условиях их распространения. Он применяется поэтому не только в оптике, но и при изучении распространения радио- и звуковых волн для определения эффективной трассы «луча», идущего от передатчика к приёмнику; для выяснения того, будут ли при данных условиях играть роль дифракционные явления; для ориентировки в вопросах о направленности излучения, фокусировке волн и т.п.

        

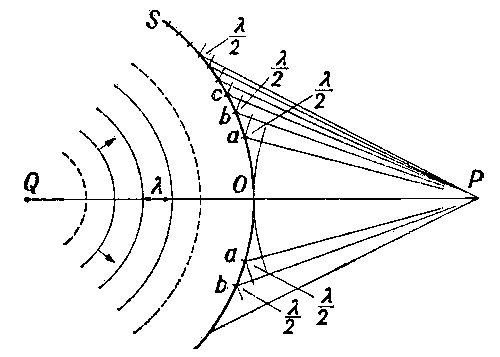        Рис. к ст. Зоны Френеля.