Вписанные и описанные фигуры
- Вписанные и описанные фигуры
-
в элементарной геометрии. Многоугольник называется вписанным в выпуклую кривую, а кривая — описанной около многоугольника, если все вершины многоугольника лежат на кривой (
рис. 1). Многоугольник называется описанным вокруг кривой, а кривая — вписанной в многоугольник, если каждая сторона многоугольника или её продолжение касается кривой. В качестве кривой чаще всего рассматривается окружность. Всякий треугольник имеет одну описанную и одну вписанную окружности (
рис. 2). Выпуклый четырёхугольник имеет описанную окружность тогда и только тогда, когда сумма противоположных углов составляет 180° (
рис. 3). Для того чтобы четырёхугольник имел вписанную окружность, необходимо и достаточно, чтобы сумма длин одной пары противолежащих сторон равнялась сумме длин другой пары (
рис. 4). Многоугольник может быть вписан в окружность, если этим свойством обладают четырёхугольники, образованные диагональю многоугольника и тремя сторонами, а также если перпендикуляры, проведённые через середины сторон, пересекаются в одной точке. Вписанная окружность существует в том и только в том случае, когда биссектрисы внутренних углов многоугольника пересекаются в одной точке. В проективной геометрии важную роль играют теоремы о шестиугольнике, вписанном в коническое сечение (см.
Паскаля теорема) и описанном около него (см.
Брианшона теорема).
В. и о. Ф. рассматриваются и в пространстве. В этом случае вместо многоугольника рассматривается многогранник, а вместо выпуклой линии — выпуклая поверхность, чаще всего сфера (рис. 5). Можно говорить также о конусе или цилиндре, вписанном в сферу, о сфере, вписанной в конус (рис. 6), и т.п.
Лит.: Перепёлкин Д. И., Курс элементарной геометрии, ч. 1—2, М. — Л., 1948—49.
Рисунок к ст. Вписанные и описанные фигуры.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Полезное
Смотреть что такое "Вписанные и описанные фигуры" в других словарях:
ВПИСАННЫЕ И ОПИСАННЫЕ ФИГУРЫ — Многоугольник наз. вписанным в выпуклую кривую, а кривая описанной около многоугольника, если все вершины многоугольника лежат на кривой (рис. 1). Многоугольник наз. описанным вокруг выпуклой кривой, а кривая вписанной (вневписанной) в… … Математическая энциклопедия
Описанные фигуры — см. Вписанные и описанные фигуры … Большая советская энциклопедия
ВПИСАННАЯ ЛОМАНАЯ — линия L, состоящая из конечного числа ппрямолинейных отрезков концы к рых расположены на данной плоской или пространственной линии Г, причем точки А;берутся в порядке возрастания параметра на кривой. Напр., частным случаем В. л. при n=2 является… … Математическая энциклопедия
ЕВКЛИД — [греч. Εὐκλείδες] (кон. IV нач. III в. до Р. Х.), древнегреч. математик и педагог, представитель александрийской математической школы, широкую известность приобрел благодаря сочинению по основам математики, озаглавленному «Начала» (Στοιχεῖα, букв … Православная энциклопедия
Планиметрия — (от лат. planum «плоскость», др. греч. μετρεω «измеряю») раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Первое… … Википедия
Площадь (в геометрии) — Площадь, одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П. было уже в древности… … Большая советская энциклопедия
Площадь — I Площадь одна из основных величин, связанных с геометрическими фигурами. В простейших случаях измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е. квадратов со стороной, равной единице длины. Вычисление П.… … Большая советская энциклопедия
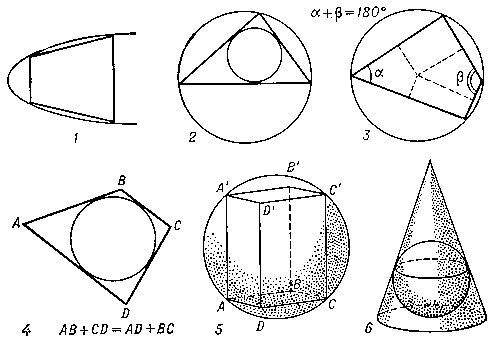 Рисунок к ст. Вписанные и описанные фигуры.
Рисунок к ст. Вписанные и описанные фигуры.