Индукция

I (греч. hypothesis — основание, предположение, от hypó — под, внизу и thésis — положение)

        то, что лежит в основе, — причина или сущность. Например, «атомы» Демокрита, «идеи» Платона, «перводвигатель» Аристотеля. В современном словоупотреблении Г. — выраженное в форме суждения (или суждений) предположение или предугадывание чего-либо: например, «предугадывание природы» в формулировке естественнонаучных законов. При этом первоначальный смысл термина «Г.» вошёл в содержание понятия «научная Г.», выражающего предположительное суждение о закономерной (или причинной) связи явлений. По выражению И. Канта, Г. — это не мечта, а мнение о действительном положении вещей, выработанное под строгим надзором разума. Являясь одним из способов объяснения фактов и наблюдений — опытных данных, Г. чаще всего создаются по правилу: «то, что мы хотим объяснить, аналогично тому, что мы уже знаем». Любая научная Г. начинается с познавательного вопроса. Например, «Если небесные тела подчиняются закону свободного падения, то каким образом возможно движение планет?". Вопрос выражает потребность познания — перейти от незнания к знанию, и возникает тогда, когда для ответа на него уже имеются некоторые данные — факты, вспомогательные теории или Г. и др. В этом смысле научная Г. по своей гносеологической роли является связующим звеном между «знанием» и «незнанием» (отсюда роль Г. в процессах научного открытия), а по своей логической роли — «формой развития естествознания, поскольку оно мыслит...» (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 555). Характеристика Г. как основной формы мысленного освоения мира отражает не только роль Г. в естествознании, но в равной мере и её роль в общественных науках. Примером может служить выдвинутая К. Марксом Г. материализма в социологии, которая, по словам Ленина, впервые возвела социологию на степень науки (см. Полн. собр. соч., 5 изд., т. 1, с. 136—37, 139—40).

         Для того чтобы быть научной, Г. должна удовлетворять следующим требованиям. 1-е требование: научная Г. должна быть (хотя бы в принципе) проверяемой, т. е. следствия, выведенные из неё путём логической дедукции (См. Дедукция), должны поддаваться опытной проверке и соответствовать (или удовлетворять) результатам опытов, наблюдений, имеющемуся фактическому материалу и т.д. Отсюда — тенденция науки придавать научной Г. точную логическую (математическую) формулировку, обеспечивающую включение Г. в качестве общего принципа в дедуктивную систему с последующим сравнением результатов дедукции с результатами наблюдений и экспериментов. Чисто логический «скелет» процедуры введения Г. в (дедуктивное) доказательство и их исключения даётся, например, правилами т. н. естественного логического вывода (см. Логика). Техника методов подтверждения Г., в частности её вероятности при данном уровне знания, исследуется в индуктивной и вероятностной логике (См. Вероятностная логика) (см. Индукция), в теории статистических решений, 2-е требование: Г. должна обладать достаточной общностью и предсказательной силой, т. е. объяснять не только те явления, из рассмотрения которых она возникла, но и все связанные с ними явления. Кроме того, она должна служить основой для вывода заключений о неизвестных ещё явлениях (свойство, характерное, в частности, для т. н. математических Г.). 3-е требование: Г. не должна быть логически противоречивой. Из противоречивой Г. по правилам логики можно вывести любые следствия, как проверяемые в смысле 1-го требования, так и их отрицания. Противоречивая Г. заведомо лишена познавательной ценности, 1-е и 2-е требования отличают научные Г. от т. н. рабочих Г., рассчитанных только на «условное объяснение» данного явления и не претендующих на отображение «действительного положения вещей». Рабочие Г. часто используются как промежуточные звенья в научных построениях благодаря их дидактической ценности.

         Лит.: Навиль Э., Логика гипотезы, СПБ, 1882; Джевонс С., Основы науки, СПБ, 1881, гл. 23; Асмус В. Ф., Гипотеза, в кн.: Логика, М., 1956; Кузнецов И. В., О математической гипотезе, «Вопросы философии», 1962, № 10; Пойа Д., Математика и правдоподобные рассуждения, пер. с англ., М., 1957; Копнин П. В., Гипотеза и познание действительности, К., 1962; Новосёлов М. М., К вопросу о корректном применении вероятностных методов при анализе мыслительных задач, «Вопросы психологии», 1963, № 2; Вилькеев Д. В., Роль гипотезы в обучении, «Советская педагогика», 1967, № 6; Баженов Л. Б., Современная научная гипотеза, в кн.: Материалистическая диалектика н методы естественных наук, М., 1968.

         Б. В. Бирюков, М. М. Новосёлов.

II Инду́кция (от лат. inductio — наведение, побуждение)

        в физиологии, динамическое взаимодействие нервных процессов — возбуждения (См. Возбуждение) и торможения (См. Торможение), выражающееся в том, что торможение в группе нервных клеток вызывает (индуцирует) возбуждение (положительная И.), и наоборот, первично вызванный процесс возбуждения индуцирует торможение (отрицательная И.). Как положительная, так и отрицательная И. могут иметь две формы: 1) одновременную (симультанную) — возбуждение в одном участке индуцирует и усиливает одновременное торможение в окружающих участках, а очаг торможения индуцирует процесс возбуждения; 2) последовательную (сукцессивную), при которой смена отношений протекает во времени — возбуждение в пункте его развития сменяется торможением после прекращения действия раздражителя, и наоборот. Степень выраженности и длительность И. зависят от силы возбуждения или торможения, от расстояния фокуса первичной активности до индуцируемого пункта и других условий. Явление И. характерно для всех отделов нервной системы. Оно ограничивает распространение (иррадиацию (См. Иррадиация)) нервных процессов и способствует их концентрации. Пример отрицательной И.: сильное раздражение слухового центра (резкий звонок) вызывает торможение в других нервных центрах, например в пищевом, что выражается в прекращении слюноотделения.

         И. В. Орлов.

         В эмбриологии — воздействие одних частей развивающегося зародыша (индукторов (См. Индукторы)) на другие его части (реагирующую систему), осуществляющееся при их контакте и определяющее направление развития реагирующей системы, подобное направлению дифференцировки индуктора (гомотипическая И.) или отличное от него (гетеротипическая И.). И. была открыта в 1901 немецким эмбриологом Х. Шпеманом при изучении образования линзы (хрусталика) глаза из эктодермы у зародышей земноводных. При удалении зачатка глаза линза не возникала. Зачаток глаза, пересаженный на бок зародыша, вызывал образование линзы из эктодермы, которая в норме должна была дифференцироваться в эпидермис кожи (рис.). Позже Шпеман обнаружил индуцирующее влияние хордомезодермы (См. Хордомезодерма) на образование из эктодермы гаструлы (См. Гаструла) зачатка центральной нервной системы — нервной пластинки; он назвал это явление первичной эмбриональной И., а индуктор — хордомезодерму — организатором. Дальнейшие исследования с удалением частей развивающегося организма и их культивированием по отдельности или в комбинации и пересадкой в чуждое им место зародыша показали, что явление И. широко распространено у всех хордовых и многих беспозвоночных животных. Осуществление И. возможно лишь при условии, что клетки реагирующей системы компетентны (см. Компетенция) к данному воздействию, т. е. способны воспринимать индуцирующий стимул и отвечать на него образованием соответствующих структур.

         В процессе развития осуществляется цепь индукционных влияний: клетки реагирующей системы, получившие стимул к дифференцировке (См. Дифференцировка), в свою очередь часто становятся индукторами для других реагирующих систем; индукционные влияния необходимы и для дальнейшей дифференцировки реагирующей системы в заданном направлении. Во многих случаях установлено, что в процессе И. не только индуктор влияет на дифференцировку реагирующей системы, но и реагирующая система оказывает на индуктор воздействие, необходимое как для его собственной дифференцировки, так и для осуществления им индуцирующего влияния, т. е. что И. — взаимодействие групп клеток развивающегося зародыша между собой. Для ряда Органогенезов показано, что в процессе И. из клеток индуктора в клетки реагирующей системы переходят вещества (индуцирующие агенты), которые участвуют в активации синтеза специфических информационных РНК, необходимых для синтеза соответствующих структурных белков в ядрах клеток реагирующей системы.

         Термином «И.» обозначают также более широкий круг явлений в индивидуальном развитии животных и растительных организмов: например, И. дифференцировки вторичных половых признаков половыми гормонами, И. линьки у личинок насекомых гормоном экдизоном, И. дифференцировки и роста растений фитогормонами (См. Фитогормоны), светом, температурой и др. факторами.

         Г. М. Игнатьева.

        

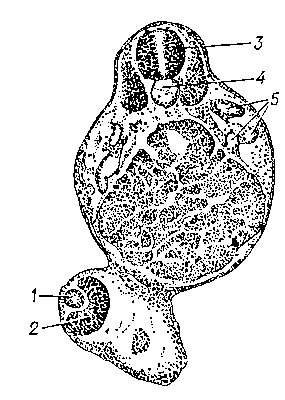        Образование линзы глаза в чуждом ему месте у зародыша обыкновенного тритона, которому был пересажен зачаток глаза альпийского тритона: 1 — индуцированная линза; 2 — пересаженный глаз; 3 — спинной мозг; 4 — хорда; 5 — почечные канальцы зародыша-реципиента.

III (греч. epagoge, лат. inductio — наведение)

        вид обобщений (См. Обобщение), связанных с предвосхищением результатов наблюдений и экспериментов на основе данных прошлого опыта. Именно поэтому и говорят об эмпирических, или индуктивных, обобщениях, или об опытных истинах, или, наконец, об эмпирических законах. Одним из оправданий И. в практике научного исследования служит познавательная необходимость общего взгляда на группы однородных фактов, позволяющего объяснять и предсказывать явления природы и общественной жизни. В И. этот общий взгляд выражается, как правило, посредством новых понятий, как бы расшифровывающих «скрытый смысл» наблюдаемых явлений, и закрепляется в формулировках причинных или же статистических законов.

         Начинается И. обычно с Анализа и сравнения (См. Сравнение) данных наблюдения или эксперимента. При этом, по мере расширения множества этих данных, может выявиться регулярная повторяемость какого-либо свойства или отношения. Наблюдаемая в опыте многократность повторения при отсутствии исключений внушает уверенность в её универсальности и естественно приводит к индуктивному обобщению — предположению, что именно так будет обстоять дело во всех сходных случаях. Если все эти случаи исчерпываются уже рассмотренными в опыте, то индуктивное обобщение тривиально и является лишь кратким отчётом о фактах. Такую И. называют полной, или совершенной, и часто рассматривают как дедукцию (См. Дедукция), так как её можно представить схемой дедуктивного умозаключения, что, в частности, делается по отношению к той идеализированной её форме, которая носит название бесконечной индукции (См. Бесконечная индукция) (см. также Математическая индукция).

         Для практики повседневного и научного мышления характерны обобщения на основе исследования не всех случаев, а только некоторых, поскольку, как правило, число всех случаев практически необозримо, а теоретическое доказательство для бесконечного числа этих случаев невозможно. Такие обобщения называются неполной И. Неполная И. уже не является логически обоснованным рассуждением. С точки зрения логики обосновать рассуждение — это найти Логический закон, соответствующий этому рассуждению, но никакой логический закон не соответствует переходу от частного к общему. С точки зрения логики справедливы только такие заключения, для получения которых не требуется никакой новой информации, кроме той, что содержится в посылках, но заключение неполной И. говорит всегда больше, чем могут сказать её посылки. В этом, собственно, познавательный смысл И. — абстрагирующая работа мысли помогает идти вперёд при недостатке практических знаний. Неполнота И. может обусловливаться не только числом посылок (неполнота в отношении числа посылок), но и их характером (неполнота в отношении характера посылок). Например, характер посылок — данных опыта — может определяться экспериментальной процедурой измерения, что, как известно, принципиально не может дать «абсолютно точных» результатов. В этом смысле неполна любая И., связанная с обобщением результатов измерений, т. е. по существу любой эмпирический закон количественной корреляции между величинами. Предполагая независимость от «сдвигов в пространстве и времени», закон является абстрактной формой выражения всеобщности в природе и тем самым бесконечности. Но по отношению к бесконечности охватываемых законом явлений наш опыт никогда не может быть закончен — нельзя пройти бесконечное. Значит И., приводящая к формулировке закона природы, неполна и в отношении посылок, и в отношении проверяемости вытекающих из него следствий, что делает её, вообще говоря, проблематичной.

         В этом видит философская критика самое слабое место неполной И. Поэтому последняя обычно рассматривается как источник предположительных суждений — гипотез (См. Индукция), которые затем проверяются иными средствами. Тем не менее положительный ответ на вопрос, следует ли стремиться к увеличению числа примеров, подтверждающих неполную И., если никакое увеличение этого числа не способно преодолеть гносеологический скептицизм, связанный с неполнотой нашего опыта, подсказывается тем, что при вполне разумных допущениях существует такое число подтверждающих примеров, при котором неполная И. с точки зрения минимизации ожидаемой потери оказывается «вполне хорошим» видом обобщения. Конечно, этот ответ является в известном смысле прагматическим и не может служить ответом на др. вопросы об основах И., например гносеологических или онтологических, которые образуют так называемую «проблему И.», ставшую предметом философских дискуссий ещё в античности.

         Из стремления решить проблему И. возникла индуктивная логика, которая самим понятием «индуктивное рассуждение» обязана Сократу, хотя И. у Сократа — это не обобщение опытных данных, а скорее метод определения — «дорога» к истинному (философскому) смыслу понятий через анализ отдельных примеров их «житейского» употребления. Лишь у Аристотеля (См. Аристотель) понимание И. связывается с обобщением наблюдений и означает, по существу, способ умозаключения, посредством которого «...общее доказывают на основании того, что известно частное» («Аналитики», 71 а1—71 а13; рус. пер., М., 1952). Этот аристотелевский взгляд восприняли философы эпикурейской школы, защищавшие И. в споре со стоиками как единственный авторитетный метод доказательства законов природы. Тогда-то и возникла впервые проблема И. В частности, в обоснование И. эпикурейцы выдвинули, как им казалось, эмпирический, а на деле вполне логический критерий: отсутствие фактов, мешающих индуктивному обобщению, — противоречащих ему примеров.

         Этот критерий, возрожденный Ф. Бэконом, стал основой той формы индуктивной логики, исторически первым вариантом которой явились индуктивные методы Бэкона — Милля. Важность противоречащего примера обусловлена тем, что наблюдения (факты), благоприятствующие индуктивному обобщению, могут лишь в той или иной степени подтверждать И., но никогда не могут иметь значения доказательств, в то время как единственный противоречащий пример, с чисто логической точки зрения, опровергает результаты И. необходимым образом. Если данные наблюдения позволяют нам выдвинуть несколько основанных на них индуктивных обобщений, или гипотез, то опровергающая сила противоречащего примера может быть использована вполне положительным образом для подтверждения одной (или нескольких) из них. Для этого только необходимо, чтобы гипотезы были альтернативными, т. е. чтобы они были связаны между собой так, что опровержение одной из них подтверждало бы остальные. Естественно тогда стремиться к созданию такой экспериментальной ситуации, которая устранит все гипотезы за исключением одной. Процесс устранения (элиминации) гипотез посредством опровергающего эксперимента был назван Дж. С. Миллем (См. Милль) исключающей, или научной, И. Если из ряда возможных гипотез опровергаются все, кроме одной, элиминация будет полной. Если же остаются несколько неопровергнутых гипотез, т. е. таких, для которых не удалось построить противоречащего примера, элиминация будет частичной. Пусть, к примеру, за группой событий ABC следует группа событий αβγ. Данные наблюдения позволяют выдвинуть ряд альтернативных гипотез: или «α есть следствие А», или «α есть следствие B», или «α есть следствие С». Какая из этих гипотез истинна? Очевидно, что эксперимент, устанавливающий, что лишь βγ являются следствиями BC, и будет опровергающим для последних двух гипотез, и элиминация будет полной.

         И Бэкон, и Милль стремились к разысканию аподиктических (необходимых) основ И. в рамках методологии Эмпиризма. Казалось, что опровергающий эксперимент служит именно такой основой. Однако, вторгаясь в область эмпирических фактов, теория опровергающего эксперимента оказывается «слишком логической», не учитывающей, во-первых, что в этом случае результаты, полученные с помощью логики, зависят от характера «внелогических» допущений и не могут превышать точность последних и, во-вторых, всегда лишь «относительную доказательность» наблюдений и экспериментов. (Для примера достаточно сравнить эксперименты О. Ж. Френеля (См. Френель) и Ж. Б. Л. Фуко, опровергающие корпускулярную «модель» света в пользу волновой, и фотоэлектрический эффект или милликеновский эксперимент по «выбиванию» электронов из мельчайших пылинок, опровергающие волновую «модель» в пользу корпускулярной.) Кроме того, дальнейший анализ миллевских методов показал, что все они являются по существу соединением приёмов дедуктивного вывода с неполной И. Если первые обеспечивают доказательную силу этим методам, то последняя её элиминирует, так что и в этом смысле степень убедительности научной И. не может превышать степень убедительности неполной И.

         Осознание этого факта привело большинство «эмпирически настроенных» исследователей к поискам вероятностных основ И. Стали предприниматься попытки свести учение об И. к учению о вероятности (См. Вероятность), а индуктивную логику — к вероятностной логике (См. Вероятностная логика). Среди наиболее систематических попыток такого рода выделяются теории, в которых вероятностной мерой оценивается лишь правдоподобность индуктивного перехода от данных наблюдения к индуктивным обобщениям, в то время как самому индуктивному обобщению не приписывается никакой вероятности: индуктивное обобщение может быть либо истинным, либо ложным — одно из двух. Можно сказать, что такой подход сохраняет принципы классической логики в ущерб некоторым принципам эмпиризма. Действительно, если наше отношение к суждениям основывается на принципе двузначности (см. Двузначности принцип), то проблематичность результатов И. должна иметь только субъективный смысл, отражающий преходящий факт нашего знания или незнания действительного, независимого от опыта, положения вещей. Если же, напротив, и в отношении посылок И., и в отношении индуктивных обобщений, и в отношении их следствий основываться исключительно на данных опыта, то при любом «вероятностном подходе» к И. законы природы должны рассматриваться лишь как более или менее вероятные гипотезы, и подтверждающие их факты должны мыслиться тоже как случайные, что уже делает всякое суждение о мире «принципиально проблематичным», лежащим вне сферы классической логики. Ссылка на «приблизительно верный» характер индуктивных обобщений не меняет дела, ибо с теоретической точки зрения малейшая неточность есть в принципе неточность абсолютная.

         Вывод о вероятностном характере законов природы в известном смысле обязан представлению, что знание «об общем» по существу индуктивно и возможно только на основе эмпирических наблюдений, эмпирические же наблюдения сами по себе недостаточны для доказательства необходимости. Однако известно, что многие из индуктивных обобщений имеют основу не только в наблюдениях, но и в чисто умозрительных принципах, вроде принципа инерции или обобщённого принципа относительности, которые входят в формулировки теорий и принимаются как аксиомы нашей научной картины мира, и с помощью которых уже чисто логическим путём выводятся как индуктивные обобщения, так и утверждения об их следствиях — наблюдаемых явлениях. Другими словами, человеческий разум не питает априорного доверия к «фактической основе» индуктивных обобщений. Большинству из них он стремится дать логическое основание, подчиняя их чисто теоретическим постулатам. Сами же эти постулаты обязаны скорее эвристической, или творческой, работе мышления, так что при любых сколько-нибудь широких индуктивных обобщениях основываются не только на данных опыта, но и демонстрируют (часто неосознанно) поразительную уверенность в способность мысли угадывать «ход природы». Объективная значимость этой чисто психологической уверенности проявляется и в вероятностной модели И.: заключение, оправдывающее поиск примеров, подтверждающих неполную И., основывается на предпосылке, что подтверждение возможно только в том случае, если индуктивное обобщение, независимо от этого подтверждения, обладает некоторой априорной правдоподобностью.

         Целесообразность доверия к индуктивным обобщениям, помимо тех оснований, которые рассматриваются в индуктивной логике, имеет ещё одно, чисто гносеологическое основание, подсказанное различием гносеологической точности эмпирического закона — его практической применимости в соответствующей (бесконечной, но всегда ограниченной) предметной области — и метрической точности его индуктивной основы. Ко времени открытия закона всемирного тяготения эмпирическая основа (наблюдения и эксперимент) позволяли И. Ньютону проверить этот закон с точностью лишь около 4%. И тем не менее, при проверке более чем два века спустя, закон оказался правильным с точностью до 0,0001%. Вообще говоря, коль скоро речь идёт о законе природы, для возрастающей в достаточно широком интервале метрической точности посылок И. гносеологическая точность обобщения (закона природы) является непрерывной в этом интервале. Поэтому было бы неразумно каждый шаг применения закона ставить в зависимость от техники измерений, хотя метрическая точность обобщения не может, разумеется, превышать метрическую точность его эмпирической основы.

         Не в каждом случае «индуктивного открытия» основа И. неадекватна той значимости, которую обычно приписывают её результатам. Например, опыт современников Ньютона был вполне достаточен для подтверждения его второго закона, даже для убеждения в его универсальной истинности. Чтобы заметить, что масса тела является функцией скорости, нужен был опыт со скоростями, почти равными скорости света, а это — опыт иной исторической эпохи. Значит, если верно, что опыт — это источник и пробный камень всех наших знаний, то это верно лишь с оговоркой, что опыт рассматривается в его исторической перспективе, как историческая практика человека, а не только как опыт «на данный день». Поскольку же «опыт на данный день» остаётся единственным эмпирическим источником обобщений, И. нуждается, по крайней мере психологически, в поддержке таких принципов, которые бы не зависели от этой основы.

         Одним из таких принципов является принцип познаваемости мира, определяющий всю целенаправленную деятельность научного мышления. Основное содержание этого принципа прекрасно выражает мысль Г. Галилея, что человеческий разум познаёт некоторые истины столь совершенно и с такой абсолютной достоверностью, какую имеет сама природа. На первый взгляд кажется, что многочисленные изменения научных воззрений и переформулировки старых законов плохо согласуются с этой мыслью. И тем не менее для жизнеспособности «старых» теорий является фундаментальным то обстоятельство, что гносеологическая точность научных абстракций, равно как и их полнота, однозначно определяются опытом в весьма широких пределах, так что с каждой научной абстракцией связан соответствующий ей интервал, внутри которого повышение точности данных опыта ничего не меняет в теоретической оценке обобщения и в его практическом использовании. Обнаружение «ошибочности» абстракции — индуктивного обобщения — есть, по существу, лишь выявление границ этого интервала, границ применимости абстракции. И хотя эти границы и неизвестны заранее, это не меняет того факта, что внутри этих границ, т. е. внутри интервала гносеологической точности абстракции, она обладает такой абсолютной достоверностью, какую имеет сама природа.

         Лит.: Энгельс Ф., Диалектика природы, Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20; Джевонс У. С., Основы науки. Трактат о логике и научном методе, пер. с англ., СПБ. 1881; Милль Д. С., Система логики силлогистической и индуктивной, пер. с англ., М., 1914; Бэкон Ф., Новый органон, пер. [с латин.], Л., 1935; Рутковский Л, В., Критика методов индуктивного доказательства, в кн.: Избранные труды русских логиков 19 в., М., 1956; Рассел Б., Человеческое познание. Его сфера и границы, пер. с англ., М., 1957; Франк Ф., Философия науки, пер. с англ., М., 1960; Котарбиньский Т., Лекции по истории логики, Избр. произв., пер. с польск., М., 1963; Уёмов А. И., Индукция и аналогия, Иваново, 1956; Лазарев Ф. В., Проблема точности естественнонаучного знания, «Вопросы философии», 1968, № 9; Пятницын Б. Н., Субботин А. Л., Соображения о построении индуктивной логики, «Вопросы философии», 1969, № 2; Карнап Р., Философские основания физики, пер. с англ., [М., 1971]; Keynes J. М., A treatise on probability, L., 1952; Nicod J., Le probleme logique de l'induction. P., 1961; Gordon М., O uspawiedliwieniu indukcji, Warsz., 1964; Induction, acceptance and rational belief, ed. by М. Swain, Dordrecht, 1970; Wright G. H., The logical problem of induction, 2 ed., Oxf., 1957.

         М. М. Новосёлов.

IV Инду́кция

        электрическая и магнитная, физические величины, характеризующие (наряду с напряжённостями электрического и магнитного полей) электромагнитное поле. В вакууме эти характеристики совпадают с соответствующими напряжённостями, если пользоваться СГС системой единиц (См. СГС система единиц) (Гаусса); в Международной системе единиц (См. Международная система единиц) (СИ) они различаются постоянными множителями.

         Вектор электрической индукции D (называемый также электрическим смещением) является суммой двух векторов различной природы: напряжённости электрического поля (См. Напряжённость электрического поля) Е — главной характеристики этого поля — и поляризации Р, которая определяет электрическое состояние вещества в этом поле. В системе Гаусса:

         D = E + 4πP (1)

         (4π — постоянный коэффициент); в системе СИ

         D = ε₀E + P, (1')

        где ε₀ — размерная константа, называемая электрической постоянной или диэлектрической проницаемостью вакуума. Вектор поляризации Р представляет собой электрический Дипольный момент единицы объёма вещества в поле Е, т. е. сумму электрических дипольных моментов p_i, отдельных молекул внутри малого объёма ΔV, деленную на величину этого объёма:

        

         В изотропном веществе, не обладающем сегнетоэлектрическими свойствами (см. Сегнетоэлектричество), при слабых полях вектор поляризации прямо пропорционален напряжённости поля. В системе Гаусса

         P = χ_еЕ, (3)

        где χ_e — безразмерная величина, называемая коэффициентом поляризации или диэлектрической восприимчивостью. Именно она характеризует электрические свойства вещества. Для сегнетоэлектриков χ_e зависит от Е, так что связь Р и Е становится нелинейной.

         Подставляя выражение (3) в (1), получим:

         D = (1 + 4πχ_е)Е = εЕ. (4)

         Величина ε = 1 + 4πχ_e, (5)

        также характеризующая электрические свойства вещества, называется диэлектрической проницаемостью (См. Диэлектрическая проницаемость). В системе СИ

         Р = χ_e ε₀E (3')

         и, соответственно,

         D = ε₀εЕ, (4’)

         ε = 1 + χ_e. (5’)

         Смысл введения вектора электрической И. состоит в том, что Поток вектора D через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами внутри объёма, ограниченного данной поверхностью, подобно потоку вектора Е. Это позволяет не рассматривать связанные (поляризационные) заряды и упрощает решение многих задач.

         Вектор магнитной индукции В — основная характеристика магнитного поля, представляющая собой среднее значение суммарной напряжённости микроскопических магнитных полей, созданных отдельными электронами и др. элементарными частицами. Вектор же напряжённости магнитного поля (См. Напряжённость магнитного поля) Н является разностью двух векторов различной природы: вектора В и вектора намагниченности (См. Намагниченность) I. В системе Гаусса

         Н = В — 4πI,

         Или

         (6)

         В = Н + 4πI.

         Намагниченность представляет собой Магнитный момент единицы объёма и характеризует магнитное состояние вещества. В изотропной среде при слабых полях намагниченность прямо пропорциональна Н:

         I = χ_m H, (7)

        где χ_m — Магнитная восприимчивость, характеризующая магнитные свойства вещества. Для ферромагнетиков χ_m зависит от Н. Подставляя (7) в (6), получим связь между В и Н :

         В = (1 + 4πχ_m)H = μН (8)

         Величина

         μ = 1 + 4πχ_m, (9)

        также характеризующая магнитные свойства вещества, называется магнитной проницаемостью (См. Магнитная проницаемость).

         В системе СИ эти формулы записываются следующим образом:

         В = μ₀H + I, (6')

         I = μ₀χ_m H, (7')

         В = μ₀μН, (8')

         μ = 1 + χ_m (9')

         Константа μ₀ называется магнитной постоянной или магнитной проницаемостью вакуума. Вектор Н вводится в теорию электромагнитного поля в связи с тем, что Циркуляция вектора Н вдоль замкнутого контура, в отличие от циркуляции вектора В, определяется движением только свободных зарядов.

         Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 5 и 11; Фриш С. Э. и Тиморева А. В., Курс общей физики, т. 2, М., 1953, гл. 15, 18.

         Г. Я. Мякишев.