- Стокса проблема
-
задача об определении внешнего гравитационного поля планеты по её внешней уровенной поверхности (См. Уровенная поверхность) S, массе внутри S и угловой скорости вращения около некоторой оси. Дж. Г. Стокс доказал разрешимость этой задачи и дал приближённое решение для сжатого сфероида с относительной ошибкой порядка квадрата его сжатия как первой краевой задачи теории потенциала. Точное решение С. п. для эллипсоида получено итальянским учёным П. Пиццетти и М. С. Молоденским (См. Молоденский). Произвольной форме S соответствуют краевое условие
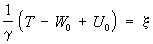 и уравнение относительно φ:
и уравнение относительно φ: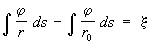 При условии
При условии где ξ — высота S над отсчётным эллипсоидом S0, содержащим заданную массу; возмущающий потенциал
где ξ — высота S над отсчётным эллипсоидом S0, содержащим заданную массу; возмущающий потенциал φ — плотность простого слоя на S, W0 — потенциал силы тяжести в начале счёта ξ на пересечении S и S0, U0 — то же на S0, γ— сила. тяжести в поле эллипсоида, r — расстояние между элементом ds и точкой на S с высотой ξ, r0 — то же между ds и точкой, являющейся началом счёта ξ. Оси вращения S и S0 совпадают. Уравнение для φ можно заменить системой линейных алгебраических уравнений. Определение φ решает задачу, именуемую С. п. Изложенное решение пригодно и в том случае, когда S — неуровенная и t, — высота квазигеоида (см. Геоид).Лит.: Молоденскиqй М. С., Еремеев В. Ф., Юркина М. И., Методы изучения внешнего гравитационного поля и фигуры Земли, М., 1960 (Тр. Центр, н.-и. института геодезии, аэросъемки и картографии, в. 131): Stokes G. G., On attractions and on Clairaut's theorem, «Cambridge and Dublin mathematical journal», 1849, v. 4.М. И. Юркина.
φ — плотность простого слоя на S, W0 — потенциал силы тяжести в начале счёта ξ на пересечении S и S0, U0 — то же на S0, γ— сила. тяжести в поле эллипсоида, r — расстояние между элементом ds и точкой на S с высотой ξ, r0 — то же между ds и точкой, являющейся началом счёта ξ. Оси вращения S и S0 совпадают. Уравнение для φ можно заменить системой линейных алгебраических уравнений. Определение φ решает задачу, именуемую С. п. Изложенное решение пригодно и в том случае, когда S — неуровенная и t, — высота квазигеоида (см. Геоид).Лит.: Молоденскиqй М. С., Еремеев В. Ф., Юркина М. И., Методы изучения внешнего гравитационного поля и фигуры Земли, М., 1960 (Тр. Центр, н.-и. института геодезии, аэросъемки и картографии, в. 131): Stokes G. G., On attractions and on Clairaut's theorem, «Cambridge and Dublin mathematical journal», 1849, v. 4.М. И. Юркина.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
