Ролля теорема — Теорема Ролля (теорема о нуле производной) утверждает, что Если функция, непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка,… … Википедия
РОЛЛЯ ТЕОРЕМА — если действительная функция f непрерывна на нек ром отрезке [а, b], имеет в каждой его внутренней точке конечную или определенного знака бесконечную производную, а на его концах принимает равные значения, то на интервале ( а, b). существует по… … Математическая энциклопедия
Теорема Ролля — (теорема о нуле производной) утверждает, что Если вещественная функция, непрерывная на отрезке и дифференцируемая на интервале , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой… … Википедия
Теорема Декарта — или правило знаков Декарта, теорема, утверждающая, что число положительных корней многочлена с вещественными коэффициентами равно числу перемен знаков в ряду его коэффициентов или на чётное число меньше этого числа (корни считаются с учётом … Википедия
Теорема Коши о среднем значении — У этого термина существуют и другие значения, см. Теорема Коши. Теорема Коши о среднем значении. Пусть даны две функции и такие, что: и определены и непрерывны на отрезке ; производные … Википедия
Ролль — (Rolle) Мишель (21.4.1652, Амбер, 8.11.1719, Париж), французский математик, член Парижской АН (с 1685). В «Трактате по алгебре» (1690) развил метод отделения действительных корней алгебраических уравнений, основанный на частном случае так … Большая советская энциклопедия
Лемма Ферма — утверждает, что производная дифференцируемой функции в точке локального экстремума равна нулю. Содержание 1 Предыстория 2 Формулировка 3 Доказательство … Википедия
Дифференциальное исчисление — раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 … Большая советская энциклопедия
Ролль, Мишель — Мишель Ролль (фр. Michel Rolle, 21 апреля 1652, Амбер (Франция) 8 ноября 1719, Париж) французский математик. Содержание 1 Биография 2 Научная деятельность … Википедия
Мишель Ролль — (фр. Michel Rolle, 21 апреля 1652, Амбер (Франция) 8 ноября 1719, Париж) французский математик. Содержание 1 Биография 2 Научная деятельность 3 С … Википедия
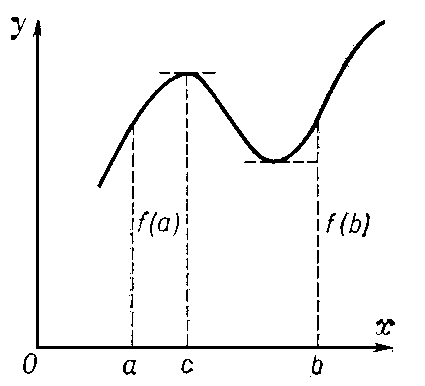Рис. к ст. Ролля теорема.